Generelt om eksponentialfunksjonar

Ein funksjon $f$ på forma $f\left(x\right)=a·b^x$ kallar vi ein eksponentialfunksjon. Talet $b$ blir kalla vekstfaktoren.

Eksponentialfunksjonar er berre definerte for positive verdiar av $b$, og vi skal berre sjå på funksjonar der også $b$ er positiv.

Funksjonane $g$ og $h$ gitt nedanfor er eksempel på eksponentialfunksjonar.

$\begin{array}{rcl}g\left(x\right)& = & 2,5·1,5^x\\ & & \\ & & D_g=\left[-4, 6\right]\\ & & \\ h\left(x\right)& =& 6,5·0,8^x\\ & & \\ & & D_h=\left[-4, 6\right]\end{array}$

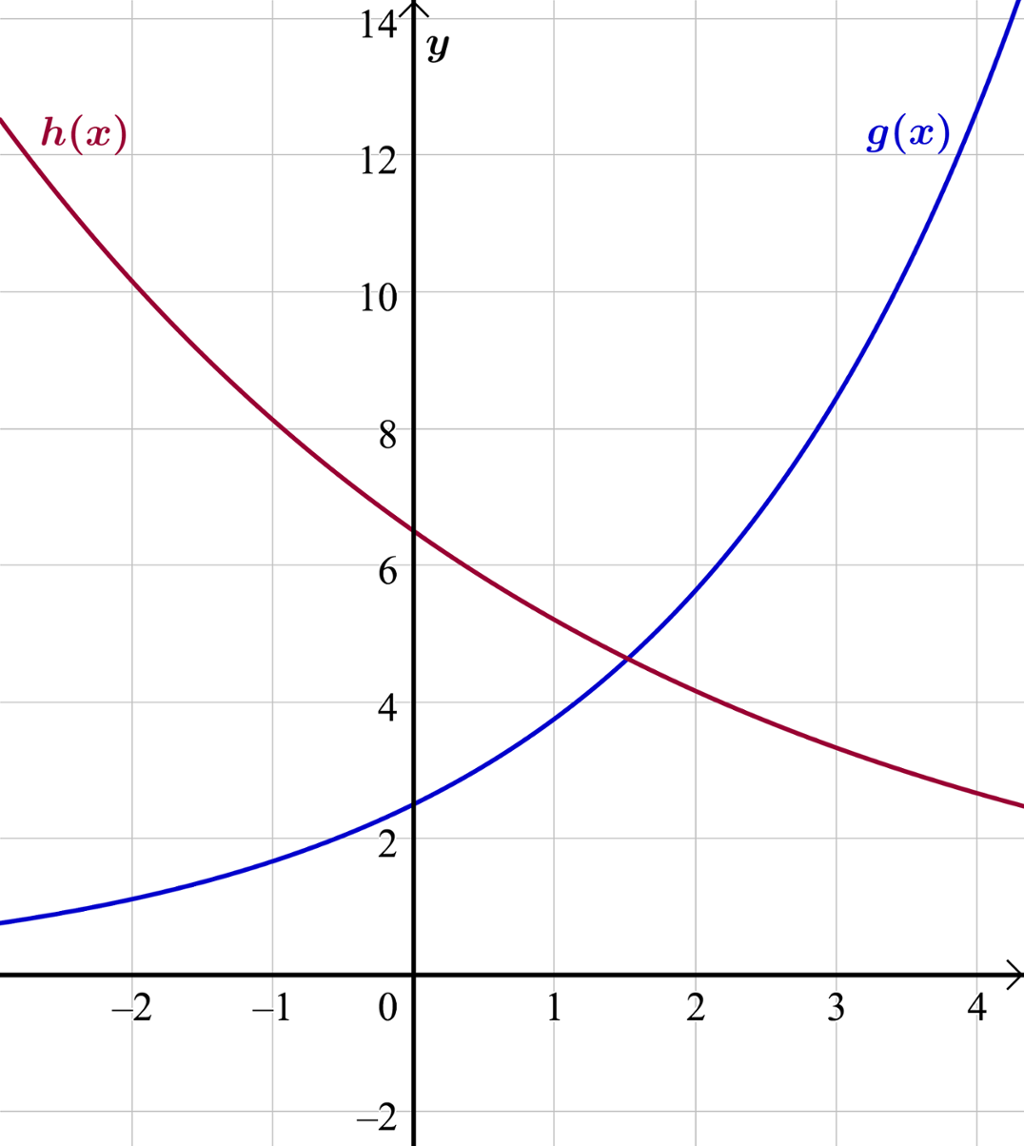
Når vekstfaktoren er større enn $1$, aukar funksjonsverdiane med ein fast prosent i like lange periodar. Samanhengen mellom den prosentvise veksten $p$ og vekstfaktoren $b$ er gitt ved likninga

$b=1+\frac{p}{100}$

Når vekstfaktoren er mindre enn $1$, minkar funksjonsverdiane med ein fast prosent i like lange periodar. Samanhengen mellom den prosentvise nedgangen $p$ og vekstfaktoren $b$ er gitt ved likninga

$b=1-\frac{p}{100}$

Talet på individ i ein populasjon i naturen vil auke eksponentielt dersom populasjonen har uavgrensa tilgang til mat og ingen fiendar. Populasjonen vil ikkje vekse så fort i byrjinga, men etter kvart vil veksten auke meir og meir. Dette er karakteristisk for eksponentiell vekst (sjå grafen av $g$ i koordinatsystemet).

Vi vil òg få eksponentiell vekst på eit bankinnskot med ei fast årleg rente.

Verdien av ein gjenstand, til dømes ein bil, vil ofte utvikle seg som ein eksponentialfunksjon med vekstfaktor mindre enn 1. Ein slik funksjon vil ha form som funksjonen $h$, sjå koordinatsystemet.