Trekanttal og Pascal sin taltrekant

Følgande figurar er komne fram ved å lage likesida trekantar av sirklar som er tettpakka.

Opne bilete i eit nytt vindauge

CC BY-NC-SA

Bilete: Olav Kristensen, Stein Aanensen

CC BY-NC-SA

Bilete: Olav Kristensen, Stein Aanensen

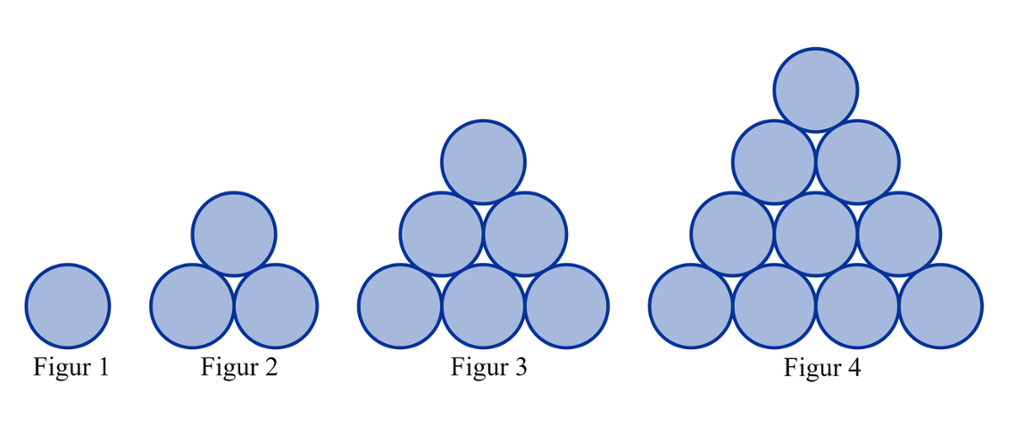
Kan du sjå kva som er mønsteret i oppbygginga av figurane?

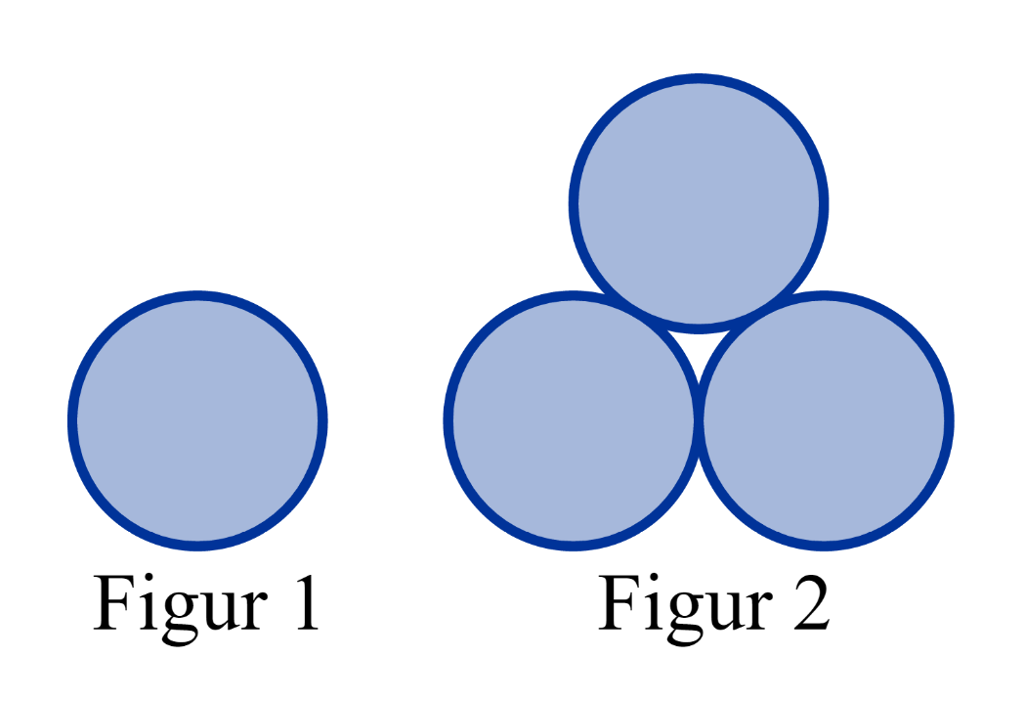
Start med figur 1 og figur 2 nedanfor, og ikkje sjå på figur 3 og figur 4 ovanfor.

Klarer du sjølv å lage figur 3 og figur 4?

Du har kanskje alt sett mønsteret. Figur 1 har 1 sirkel. Figur 2 har 2 sirklar fleir enn figur 1. Figur 3 har 3 sirklar fleir enn figur 2. Slik held det fram.

Vi får då at i figur 1 er det 1 sirkel. I figur 2 er det 1 + 2 = 3 sirklar. I figur 3 er det
1 + 2 + 3 = 6 sirklar. I figur 4 er det 1 + 2 + 3 + 4 = 10 sirklar og så vidare.

Tala 1, 3, 6, 10 og så vidare kallar vi for trekanttala. Kvifor trur du dei har fått dette namnet?

La $T\left(n\right)$ være trekanttall nummer $n$. Da er

$T\left(1\right)=1, T\left(2\right)=3, T\left(3\right)=6$ og $T\left(4\right)=10$?

Tenk no at vi lagar figur 5, figur 6 og så vidare etter same mønster. Ser du at

$T\left(5\right)=T\left(4\right)+5=15$ og $T\left(6\right)=T\left(5\right)+6=15+6=21$?

Ser du at vi generelt får $T\left(n\right)=T(n-1)+n$?

Forsøk å lage ein tabell med dei første 12 trekanttala. Kontroller med tabellen nedanfor.

Vi får til dømes at $T\left(7\right)=28=1+2+3+4+5+6+7=\frac{1+7}{2}·7$.

Brøken $\frac{1+7}{2}=4$ er gjennomsnittet av tala frå og med 1 til og med 7. Når vi multipliserer dette talet med talet på tal, som er 7, får vi summen av tala frå og med 1 til og med 7.

Det tyder at formelen $T\left(n\right)=\frac{1+n}{2}·n$ gir trekanttal nummer $n$. Kontroller at denne formelen stemmer for dei andre trekanttala.

Eit kvadrattal er eit tal du får, når du opphøgjer eit heilt tal i andre potens. Kva slags tal får du når du legg saman to «nabo-trekanttal»?

CC BY-NC-SA

Bilete: NTB scanpix, Science Photo Library

Blaise Pascal var ein kjend fransk matematikar, fysikar, oppfinnar og filosof som levde på 1600-talet. Ein spesiell taltrekant har fått namnet etter Pascal, sjølv om trekanten var kjend i mange hundre år før Pascal levde.

Opne bilete i eit nytt vindauge

CC BY-NC-SA

Bilete: Stein Aanensen, Olav Kristensen

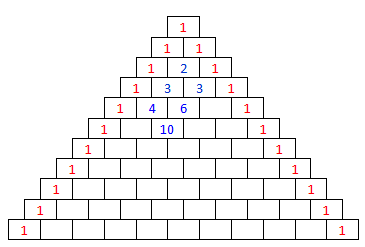
Lag ein trekant av ruter som figuren ovanfor viser. Skriv inn talet 1 i alle rutene langs kanten av trekanten. Vi har byrja å fylle inn tal i resten av rutene. Ser du korleis vi har funne desse tala? Hald fram etter same mønster, og fyll inn tal i alle rutene.

I trekanten ovanfor har vi valt å lage 11 rader. Trekanten kan utvidast etter same mønster.

Opne bilete i eit nytt vindauge

CC BY-NC-SA

Bilete: Olav Kristensen, Stein Aanensen

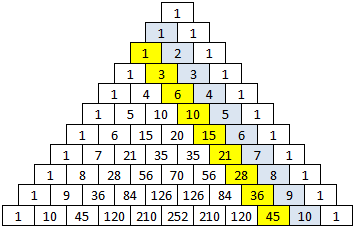
Sjå på tala som er farga gule. Kjenner du att denne talfølgja? Ganske rett. Det er trekanttala!

Ser du korleis dei kjem fram etter dette mønsteret?

$\begin{array}{l}1=1 \\ 1+2=3 \\ 1+2+3=3+3=6 \\ 1+2+3+4=6+4=10\\ 1+2+3+4+5=10 + 5=15 \\ 1+2+3+4+5+6=15+6=21\end{array}$