Nullpunkt, toppunkt, botnpunkt og symmetrilinje

CC BY-NC-SA

Bilete: Stein Aanensen, Olav Kristensen

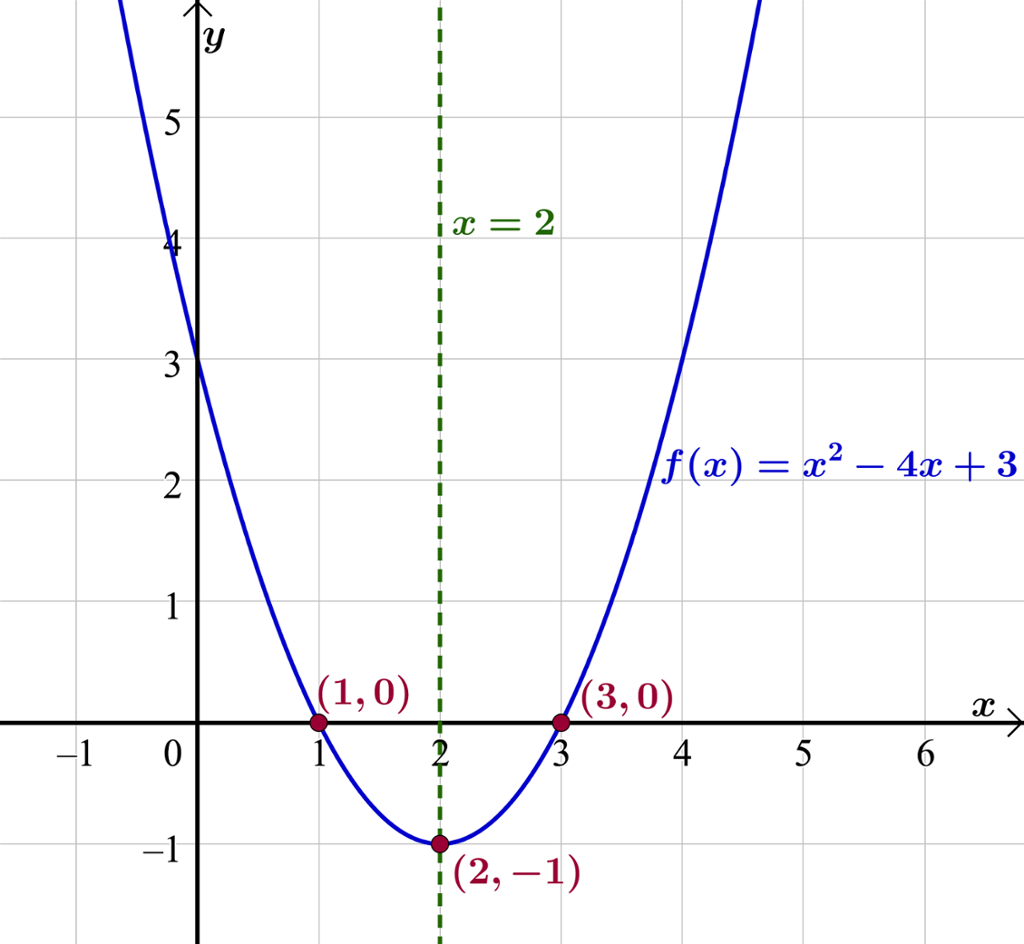
Vi teiknar grafen til funksjonen $f\left(x\right)=x^2-4x+3$ i GeoGebra og finn nullpunkta med kommandoen «Nullpunkt[f]».

Grafen har eit botnpunkt, sidan andregradsleddet er positivt. Vi finn botnpunktet med kommandoen «Ekstremalpunkt[f]». Grafen har botnpunkt $\left(2, -1\right)$.

I koordinatsystemet har vi teikna inn symmetrilinja til $f$, linja $x=2$.

Vi ser at botnpunktet ligg på symmetrilinja. Symmetrilinja ligg også like langt frå kvart av parabelen sine nullpunkt.

Vi har sett at vi kan finne parabelen sine nullpunkt ved å løyse likninga $f\left(x\right)=0$.

$\begin{array}{}\end{array}$$\begin{array}{rcl}{x}^2-4x+3& = & 0\\ & & \\ x& =& \frac{-\left(-4\right)\pm \sqrt{{\left(-4\right)}^2-4·1·3}}{2·1}\\ & & \\ x& =& \frac{4\pm \sqrt{16-12}}{2}\\ & & \\ x& =& \frac{4\pm 2}{2}\\ & & \\ x& =& 2\pm 1\end{array}$

Dersom vi stanser der, ser vi at $x=2\pm 1$.

Det tyder at dei to nullpunkta ligg like langt frå linja $x=2$, og denne linja er altså parabelen si symmetrilinje.

Generelt er nullpunkta gitt ved

$\begin{array}{rcl}x& = & \frac{-b\pm \sqrt{b^2-4ac}}{2a}\\ & & \\ & =& \frac{-b}{2a}\pm \frac{\sqrt{b^2-4ac}}{2a}\end{array}$

Det betyr at vi kan finne symmetrilinja og $x$-koordinaten til topp- eller botnpunktet ved å «fjerne» kvadratrota i uttrykket vi får når vi set $f\left(x\right)=0$.

Det betyr at vi kan finne mykje informasjon om grafen til ein andregradsfunksjon ved enkel rekning utan å bruke digitale hjelpemiddel.

CC BY-NC-SA

Bilete: Stein Aanensen, Olav Kristensen

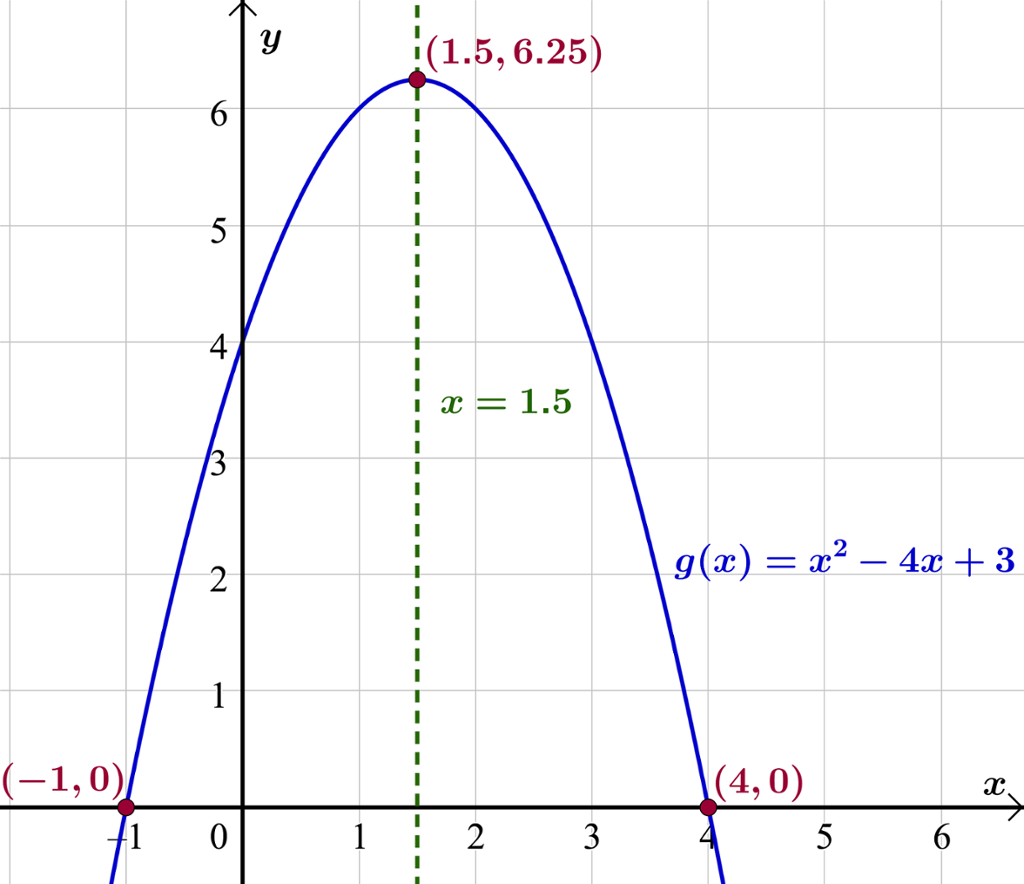
Gitt funksjonen $g\left(x\right)=-x^2+3x+4$. Finn nullpunkta til funksjonen.

$\begin{array}{rcl}g\left(x\right)& = & 0\\ & & \\ -x^2+3x+4& =& 0\\ & & \\ x& =& \frac{-3\pm \sqrt{3^2-4·\left(-1\right)·4}}{2·\left(-1\right)}\\ & & \\ x& =& \frac{-3\pm \sqrt{25}}{-2}\\ & & \\ x& =& -1 \vee x=4\end{array}$

Funksjonen har nullpunkt for $x=-1$ og for $x=4$.

Symmetrilinja er gitt ved

$x=\frac{-b}{2a}=\frac{-3}{2·\left(-1\right)}=\frac{3}{2}=1,5$

Vi ser at dette er $x$-verdien midt mellom $-1 \mathrm{og} 4$.

Grafen har eit toppunkt, sidan andregradsleddet er negativt.
Toppunktet har koordinatane

$\begin{array}{rcl}\left(1.5, g(1.5)\right)& = & \left(1.5, \left(-1.5^2+3·1.5+4\right)\right)\\ & & \\ & =& \left(1.5, (-2.25+4.5+4)\right)\\ & & \\ & =& \left(1.5, 6.25\right)\end{array}$

CC BY-NC-SA

Bilete: Stein Aanensen, Olav Kristensen

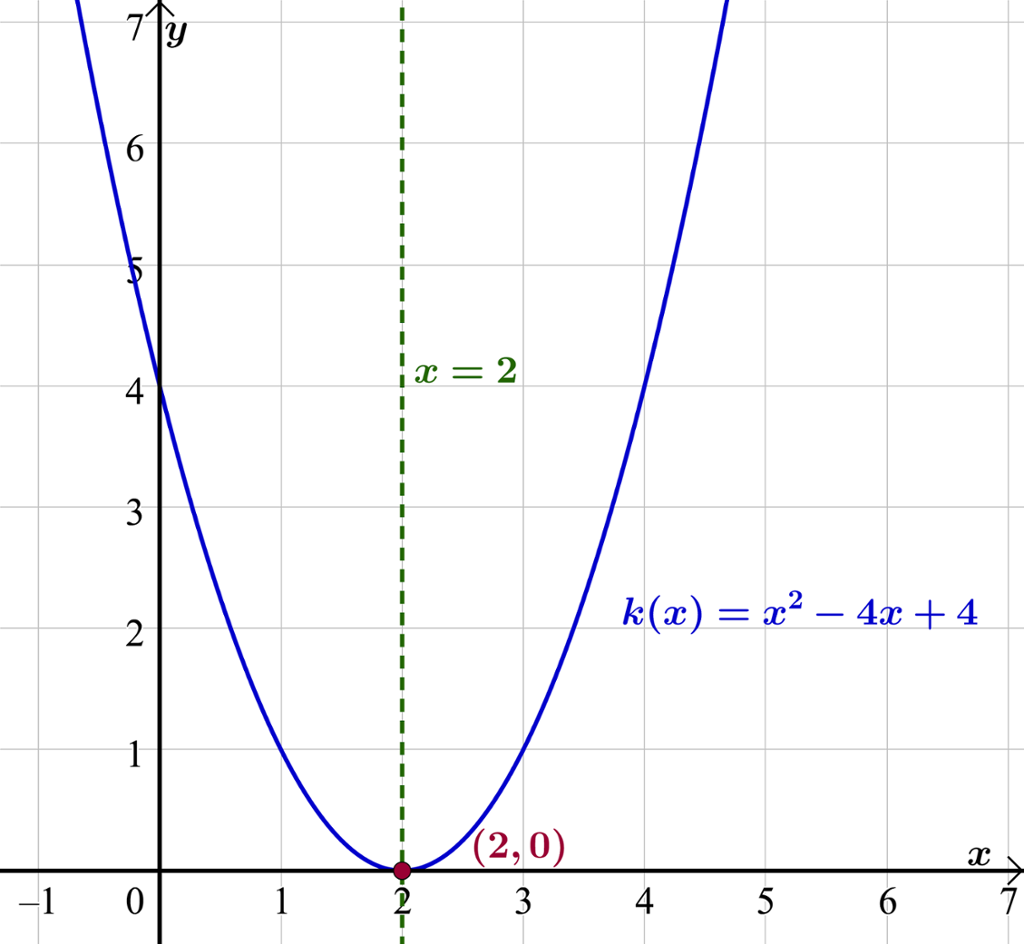
Gitt funksjonen $h\left(x\right)=x^2-4x+4$. Finn eventuelle nullpunkt til funksjonen.

$\begin{array}{rcl}h\left(x\right)& = & 0\\ & & \\ x^2-4x+4& =& 0\\ & & \\ x& =& \frac{-\left(-4\right)\pm \sqrt{{\left(-4\right)}^2-4·1·4}}{2}\\ & & \\ x& =& \frac{-\left(-4\right)\pm \sqrt{0}}{2}=2\end{array}$

Nullpunktet er $x=2$.

Vi får berre eitt nullpunkt, sidan uttrykket under kvadratrota blir lik null.

Symmetrilinja er gitt ved

$x=\frac{-b}{2a}=\frac{-\left(-4\right)}{2·1}=\frac{4}{2}=2$.

Grafen har eit botnpunkt, sidan andregradsleddet er positivt. Nullpunktet fell saman med botnpunktet og ligg på symmetrilinja.

Vi veit at $h\left(2\right)=0$. Botnpunktet har koordinatane $\left(2, h\left(2\right)\right)=\left(2, 0\right)$.

CC BY-NC-SA

Bilete: Stein Aanensen, Olav Kristensen

Gitt funksjonen $k\left(x\right)=x^2-4x+5$.

Finn eventuelle nullpunkt til funksjonen.

$\begin{array}{rcl}k\left(x\right)& = & 0\\ & & \\ x^2-4x+5& =& 0\\ & & \\ x& =& \frac{-\left(-4\right)\pm \sqrt{{\left(-4\right)}^2-4·1·5}}{2}\\ & & \\ x& =& \frac{-\left(-4\right)\pm \sqrt{-4}}{2}\end{array}$

Vi får eit negativt tal under rotteiknet. Likninga har inga løysing. Det tyder at funksjonen ikkje har nullpunkt, og grafen av funksjonen kryssar aldri $x$-aksen.

Sidan konstantleddet $c=5$, veit vi at grafen skjer $y$-aksen i punktet $\left(0, 5\right)$. Dette punktet ligg over $x$-aksen. Grafen ligg då over $x$-aksen for alle verdiar av $x$.

Vi finn symmetrilinja ved

$x=\frac{-b}{2a}=\frac{-\left(-4\right)}{2}=\frac{4}{2}=2$.

Grafen har eit botnpunkt, sidan andregradsleddet er positivt.
Botnpunktet har koordinatane $\left(2, k\left(2\right)\right)=\left(2, 2^2-4·2+5\right)=\left(2, 1\right)$.