Generelt om rasjonale funksjonar
Ein rasjonal funksjon er ein funksjon som kan skrivast som ein brøk der teljaren og nemnaren er polynom.
Eksempel
Funksjonen gitt ved er ein rasjonal funksjon.
Ein brøk er ikkje definert når nemnaren er lik null. Det betyr at ikkje eksisterer. Grafen har ikkje noko punkt for . Vi seier at grafen har eit brot for .
Vi teiknar grafen av i GeoGebra og skriv også inn kommandoen Asymptote[f].
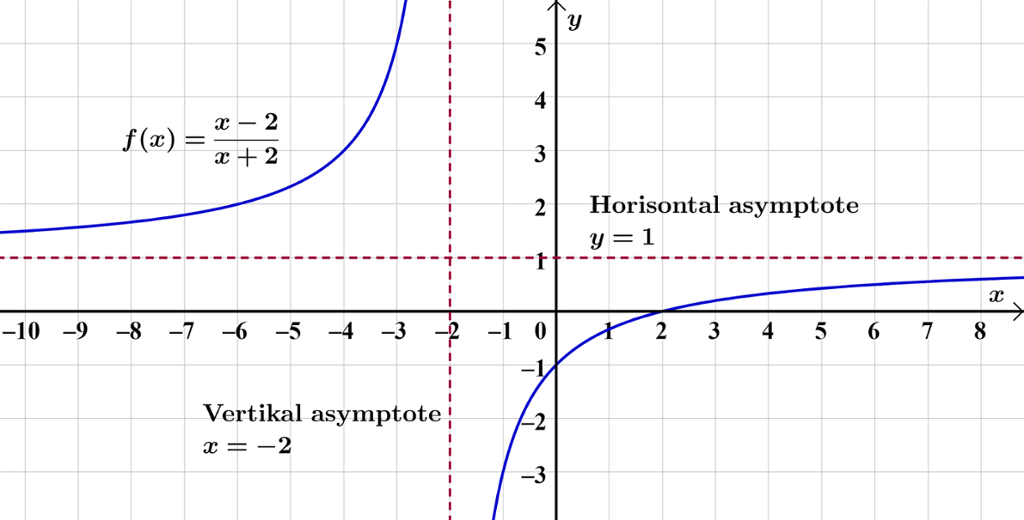
Legg merke til at grafen er symmetrisk om skjeringspunktet mellom asymptotane.
Når nærmar seg verdien frå venstre, kan det sjå ut som om funksjonsverdiane veks over alle grenser.
Det kan visast at dette er riktig. Funksjonsverdiane nærmar seg ikkje ein bestemt verdi når nærmar seg verdien frå venstre, men blir uendeleg store.
Vi skriv
når
Vi les " går mot uendeleg når går mot frå venstre".
Tilsvarande viser det seg at funksjonsverdiane søkk mot minus uendeleg når nærmar seg frå høgre. Vi skriv
når
Legg merke til og som markerer om nærmar seg frå venstre eller frå høgre.
Du kan undersøkje om dette er sannsynleg ved å setje inn verdiar for som er veldig nær .
Grafen av består av to delar, ein del til venstre for linja og ein del til høgre for linja . Linja kallar vi ein loddrett eller vertikal asymptote.
Det kan vidare visast at grafen «flatar ut» og nærmar seg linja når går mot pluss eller minus uendeleg. Det vil seie at funksjonsverdiane nærmar seg verdien som grenseverdi når går mot pluss eller minus uendeleg, men utan nokon gong å bli lik .
Den eine delen av grafen nærmar seg linja ovanfrå og den andre delen nedanfrå. Dei to delane av grafen vil aldri krysse linja. Linja er ein vassrett eller horisontal asymptote.