Korleis teikne grafen av ein andregradsfunksjon utan bruk av digitale verktøy

Gitt andregradsfunksjonen $g\left(x\right)=x^2-4x+3 , D_g=\mathrm{ℝ}$

Vi startar med å finne symmetrilinje, botnpunktet
og eventuelle nullpunkt.

$\begin{array}{rcl} g\left(x\right)& = & 0\\ & & \\ x^2-4x+3& =& 0\\ & & \\ x& =& \frac{-\left(-4\right)\pm \sqrt{{\left(-4\right)}^2-4·1·3}}{2·1}\\ & & \\ x& =& \frac{4\pm \sqrt{4}}{2}=\frac{4\pm 2}{2}\end{array}$

Nullpunkta blir

$x=\frac{4+2}{2}=3 \wedge x=\frac{4-2}{2}=1$

Symmetrilinja er

$x=\frac{4}{2}=2$

Grafen har eit botnpunkt sidan andregradsleddet er positivt. I botnpunktet er

$x=2 \wedge y=g\left(2\right)=2^2-4·2+3=-1$

Det vil seie at botnpunktet er $\left(2,-1\right)$.

I tillegg viser funksjonsuttrykket at grafen skjer $y$-aksen i punktet $(0, 3)$.

Informasjonen samlast i ein verditabell.

Symmetrilinje og minimalverdi.

Vi reknar ut $g\left(5\right)=5^2-4·5+3=8$.

På grunn av symmetri er $g\left(-1\right)=g\left(5\right)=8$ og $g\left(4\right)=g\left(0\right)=3$.

Det gir verditabellen:

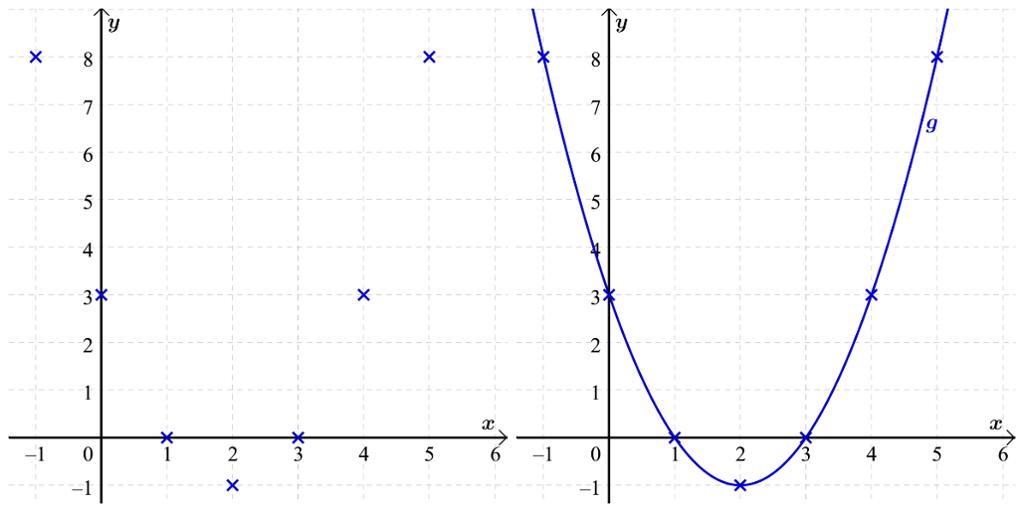
Vi har no nok av punkt og kan teikne grafen av $g$.

Vi startar med å markere punkta i eit koordinatsystem, og trekkjer så ei kurve gjennom punkta.

Opne bilete i eit nytt vindauge

CC BY-NC-SA

Bilete: Stein Aanensen, Olav Kristensen