Potensfunksjonar

CC BY-NC-SA

Bilete: Keith Leighton

Live arvar $300 000$ kroner. Ho vil spare pengane.

Den lokale banken tilbyr ei årleg rente på $3\%$ per år. Dette svarar til ein vekstfaktor på $1,03$. Live reknar det som sannsynleg at ho vil få bruk for pengane om $10$ år. Kor mykje vil beløpet ha vakse til etter $10$ år?

$300 000·1,{03}^{10}=403 175$

Beløpet vil ha vakse til ca. $403 175$ kroner.

Live veit at det finst alternativ til banksparing, og ho vil undersøkje kva beløpet kan vekse til etter $10$ år, dersom renta er høgare enn $3\%$.

Ho ser då at ho kan bruke funksjonen $B$ gitt ved

$B\left(x\right)=300 000·x^{10}$

Her er det vekstfaktoren som er den variable , $x$.

Live teiknar grafen av $B$ for $x\in \left[1.03, 1.12\right]$.

Opne bilete i eit nytt vindauge

CC BY-NC-SA

Bilete: Olav Kristensen, Stein Aanensen

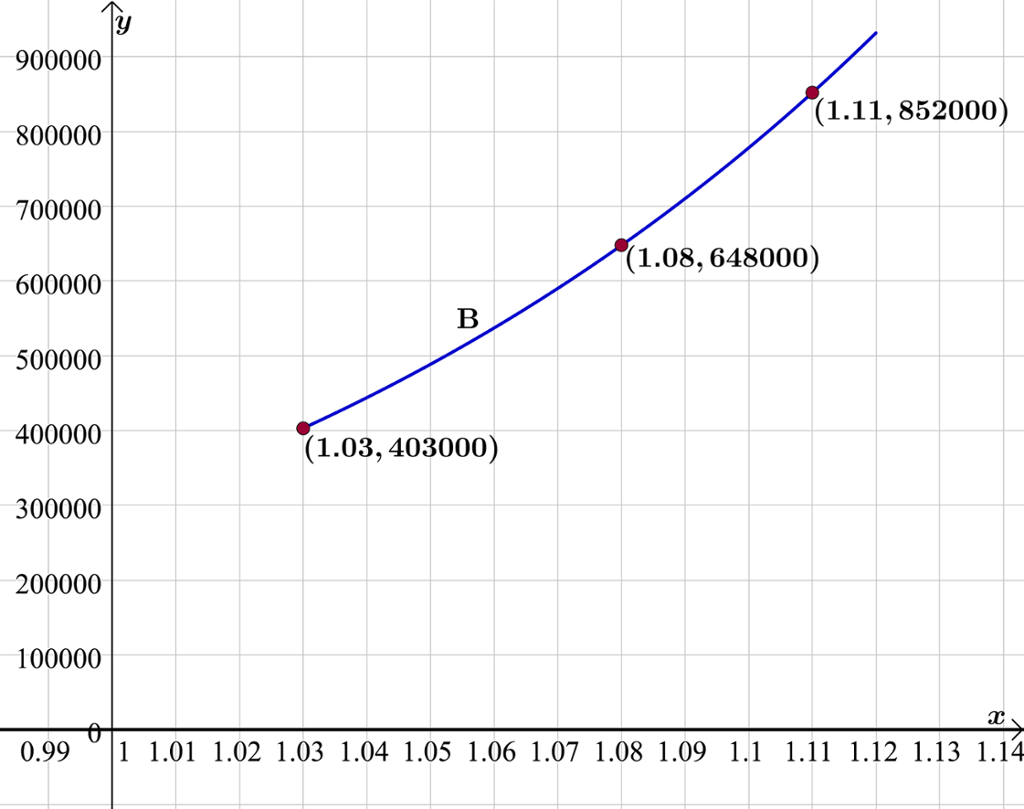
Av grafen kan ho sjå at ved ei årleg rente på $3\%$, vil beløpet vekse til ca. $403 000$ kroner etter $10$ år. Dersom renta er på $8\%$ per år, vil beløpet vekse til ca. $648 000$ kroner og dersom ho kan få ei rente på $11\%$ per år, altså at vekstfaktoren er $1,11$, vil ho sitje med ca. $852 000$ etter $10$ år.

I funksjonsuttrykket $B\left(x\right)=300 000·x^{10}$ er $x$ grunntalet i ein potens der eksponenten er eit konstant tal. Ein slik funksjon kallar vi ein potensfunksjon.

Legg merke til at når $b$ er eit ikkjenegativt heilt tal, er potensfunksjonen også ein polynomfunksjon, som til dømes $2x, 3x^2$ , osb.

Når $b$ er eit negativt heilt tal, er potensfunksjonen ein rasjonal funksjon, som til dømes $x^{-4}=\frac{1}{x^4}, 2x^{-1}=\frac{2}{x}$ osb.

Når $b$ ikkje er eit heilt tal, må vi føresetje at $x$ er positiv. Grunnen er at til dømes $x^{0,5}$ tyder det same som $\sqrt{x}$ , og kvadratrota av eit negativt tal er ikkje eit reelt tal.

Nedanfor har vi teikna grafane til nokre funksjonar gitt på formen $2x^b$. I tillegg kan du dra i glidaren for å sjå korleis potensfunksjonen ser ut for andre verdiar av $b$.

Kvifor går alle grafane gjennom punktet $\left(1, 2\right)$?

Korleis ser grafen ut når $b=1$?

Grafane endrar hovudform etter om $b\in ⟨\leftarrow , 0⟩$, $b\in ⟨0, 1⟩$ eller $b\in ⟨1, \to ⟩$.

Legg merke til at grafen av ein potensfunksjon $f$ gitt ved $f\left(x\right)=a·x^b$ alltid går gjennom punktet $\left(1, a\right)$ fordi $f\left(1\right)=a·1^b=a$.

CC BY-NC-SA

Bilete: th foto-werbung

Når ein pendel svingar, er svingetida, det vil seie den tida det tar frå vi slepper pendelen til han kjem tilbake til utgangspunktet, avhengig av lengda på snora som pendelkula heng i.

Frå naturfag kjenner du kanskje formelen for svingetida T sekund, som funksjon av snorlengda $x$ meter?

Formelen gir at

CC BY-NC-SA

Bilete: Stein Aanensen, Olav Kristensen

$T=\frac{2\pi }{\sqrt{g}}·\sqrt{x}=\frac{2\pi }{\sqrt{g}}·x^{0,5}$

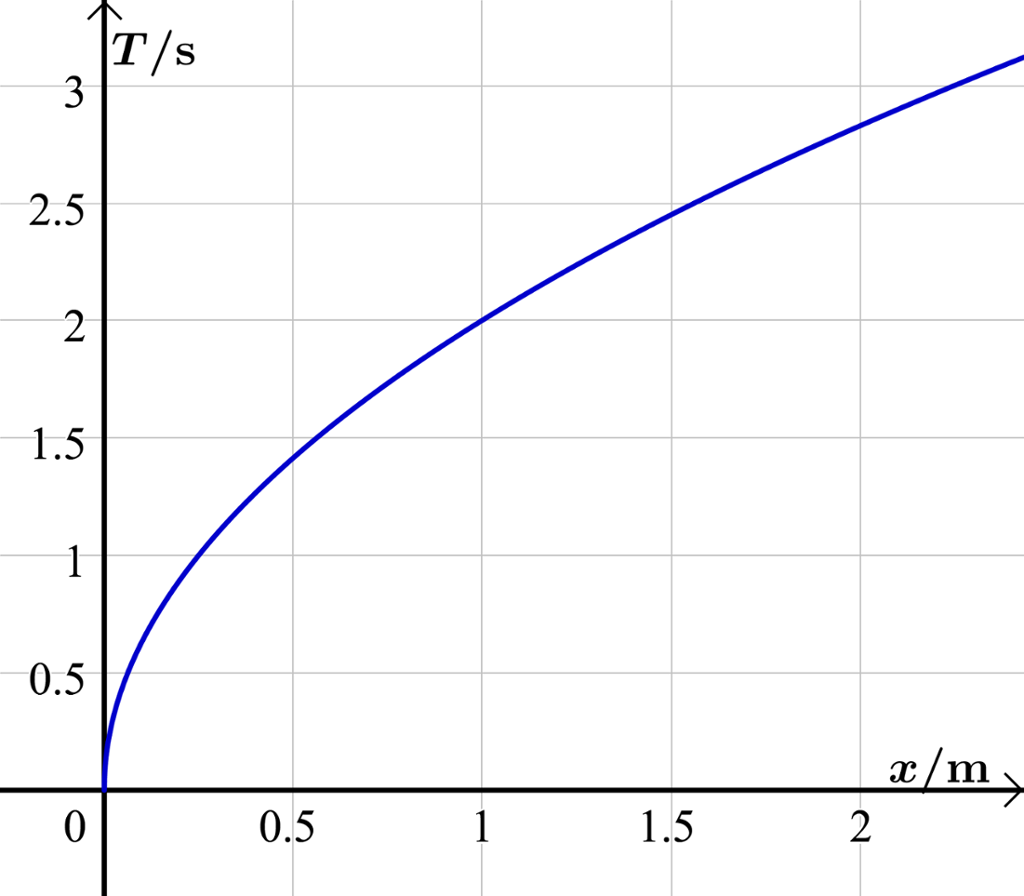
Her er $\pi \approx 3,14$ og $g\approx 9,81$ ($g$ er tyngdeakselerasjonen).

Når vi set inn desse verdiane i formelen, får vi

$T\approx \frac{2·3,14}{\sqrt{9,81}}·x^{0,5}=2,0·x^{0,5}$

Svingetida til ein pendel er altså ein potensfunksjon av snorlengda.

Vi veit også at $x^{0,5}=\sqrt{x}$, slik at svingetida kan uttrykkast som

$T=2\sqrt{x}$

Nå er svingetida uttrykt som ein funksjon.