Definisjon av bestemt integral som grenseverdi
Vi ser på funksjonen gitt ved
Nedanfor har vi teikna grafen til i eit koordinatsystem. Vi skal sjå korleis vi kan finne arealet, , av det området som er farga blått.
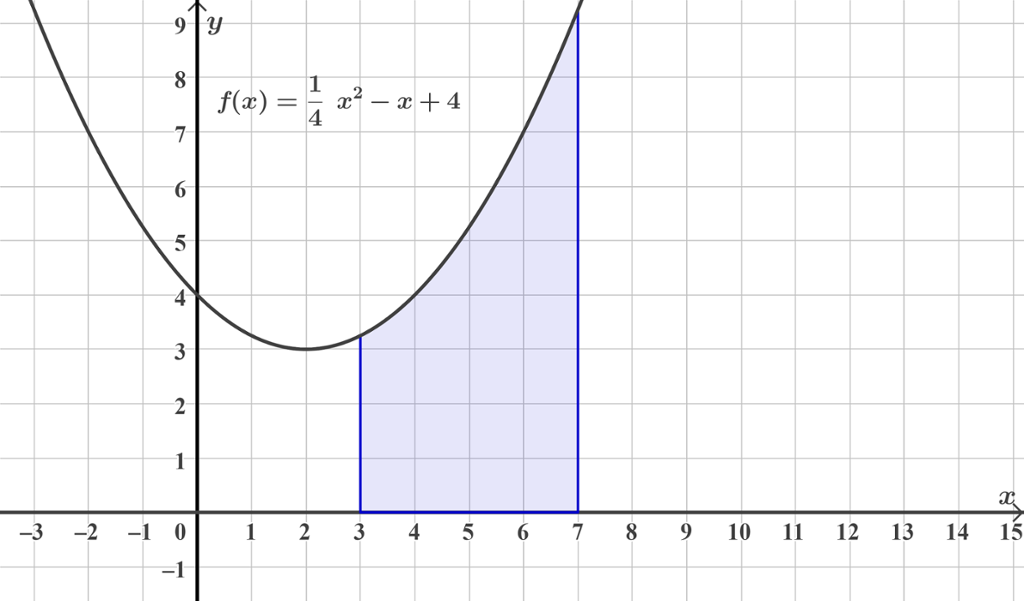
Det blå området er avgrensa av grafen til
I GeoGebra kan du legge inn funksjonen og få fram rektangla med kommandoen Sumunder(f, 3, 7, 4). Tala 3 og 7 er nedre og øvre grense langs
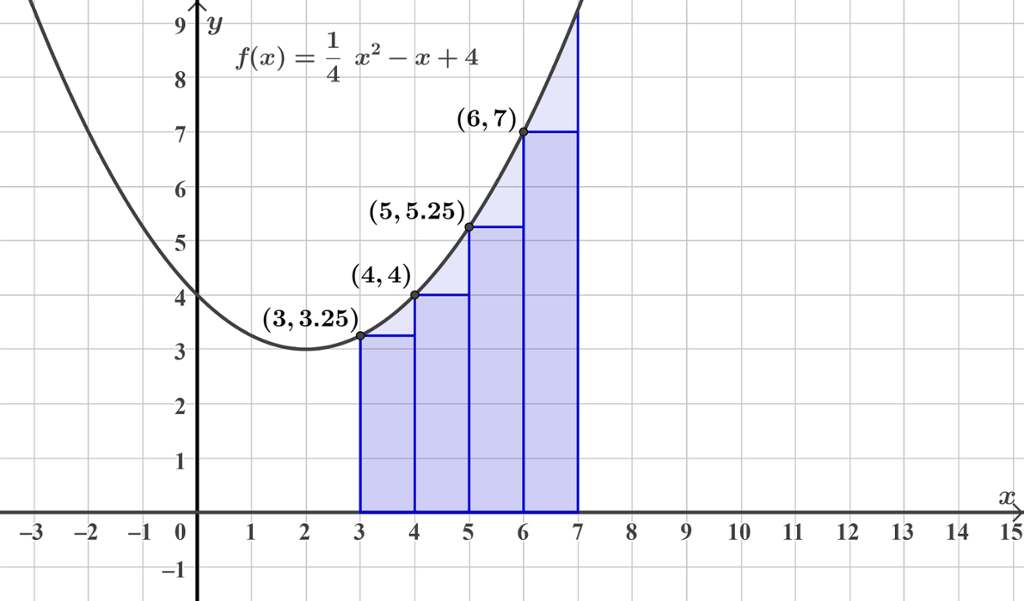
Vi ser at breidda av alle rektangla i tilfellet vårt er 1, mens høgda varierer. Høgda er gitt ved funksjonsverdien for kvar av
Vi kallar summen av dei fire rektangla for
Vi ser tydeleg av figuren ovanfor at det samla arealet av dei fire rektangla er mindre enn arealet av heile det blå området. Vi manglar dei fire "nestentrekantane" mellom grafen og dei fire rektangla.
Men vi kan likevel seie at
For å få ei betre tilnærming kan vi dele området i stadig fleire rektangel. I GeoGebra kan du auke talet på rektangel, det vil seie at du aukar det siste talet i kommandoen Sumunder(). I det interaktive GeoGebra-arket nedanfor kan du endre talet på rektangel ved å dra i glidaren. Kva skjer med arealet av alle rektangla når talet på rektangel aukar?
Filer
Vi ser at rektangla dekker meir og meir av det blå området jo fleire rektangel vi lagar.
Vi tenker oss at vi held fram med å auke talet på rektangel "i det uendelege". Breidda til rektangla, som vi kallar
Denne summen kallar vi for ein Riemann-sum, kalla opp etter den tyske matematikaren Bernhard Riemann, som presenterte denne definisjonen i 1854.
Vi bruker den greske bokstaven
For å markere grenseverdien for denne summen når
Vi får då at arealet under grafen kan skrivast som
Det er dette uttrykket som blir definert som det bestemte integralet av
Det bestemte integralet frå
Geometrisk vil det bestemte integralet
Ein annan måte å finne ein tilnærma verdi for arealet Trapessum(f, 3, 7, n), der verdien av
Filer
Dersom vi deler det området i fire trapes, vil arealet av det første trapeset vere gitt ved
Summen av areala til dei fire trapesa blir ut frå dette
Dette uttrykket kan forenklast slik:
Generelt kan vi seie at trapesmetoden går ut på å gjere ei tilnærming av integralet