Grafisk løysing av likningssett
3.2.60
Løys likningssetta grafisk.
a)
vis fasit
Vi ordnar kvar likning og skriv som ein funksjon av :
Så teiknar vi grafane og finn skjeringspunktet:
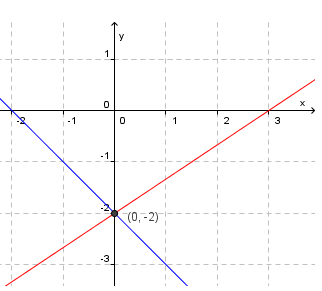
Løysing på likningssettet er
b)
vis fasit
Vi ordnar kvar likning og skriv som ein funksjon av :
Så teiknar vi grafane og finn skjeringspunktet:
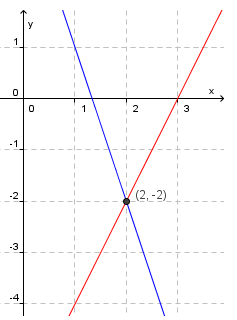
Løysing på likningssettet er .
c)
vis fasit
Vi ordnar kvar likning og skriv som ein funksjon av :
Så teiknar vi grafane og finn skjeringspunktet:
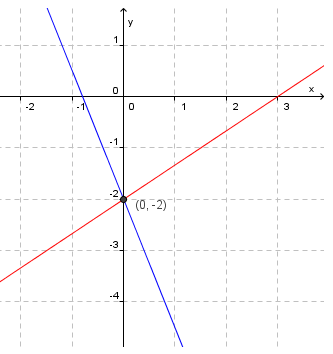
Løysing på likningssettet er
d)
vis fasit
Vi ordnar kvar likning og skriv som ein funksjon av :
Grafane får same funksjonsuttrykk. Det vil seie at dei faller saman Alle punkt som ligg på linja er løysingar av likningssettet.
e)
vis fasit
Vi ordnar kvar likning og skriv som ein funksjon av :
Så teiknar vi grafane og finn skjeringspunktet:
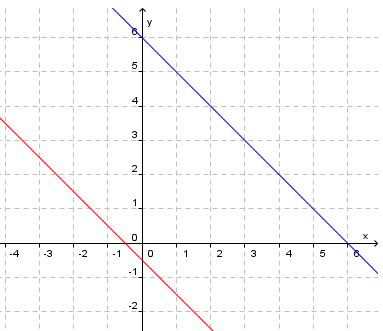
Siden linjane har same stigningstal og ulikt konstantledd er dei parallelle og vil ikkje skjere kvarandre. Likningssettet har inga løysing.