Alternative metodar til å finne likninga til ei rett linje

Du får oppgitt at ei rett linje har stigingstal $a=2$ og går gjennom punktet $\left(1, -3\right)$.

Finn likninga for linja.

Alternativ 1. Vi brukar eittpunktsformelen

Vi sett inn koordinatane til det oppgitte punktet og verdien for stigingstalet i eittpunktsformelen

$\begin{array}{rcl}y-y_1& = & a\left(x-x_1\right)\\ & & \\ y-\left(-3\right)& =& 2\left(x-1\right)\\ & & \\ y+3& =& 2x-2\\ & & \\ y& =& 2x-5\end{array}$

Vi har funne likninga for linja.

Alternativ 2. Vi brukar at generell likning for ei rett linje er

$y=ax+b$

$a=2$ gir at likninga blir $y=2x+b$.

Punktet $\left(1, -3\right)$ ligg på linja og er difor ei løysing av likninga.

Vi set inn i likninga og får

$\begin{array}{rcl}-3& = & 2·1+b\\ & & \\ b& =& -3-2=-5\end{array}$

Likninga for linja blir $y=2x-5$

Alternativ 3. Grafisk løysing

Avsett det kjente punktet i eit koordinatsystem, anten for hand eller digitalt. Bruk stigingstalet til å finne eit nytt punkt på linja. Trekk linja gjennom punkta og les av kvar grafen skjer $y$-aksen. Du har då funne konstantleddet og såleis også likninga for linja.

Ei rett linje går gjennom punkta $\left(-2, -3\right)$og $\left(1, 3\right)$.

Finn likninga for linja.

Alternativ 1. Vi brukar eittpunktsformelen

Vi finn først stigingstalet

$a=\frac{y_2-y_1}{x_2-x_1}=\frac{3-\left(-3\right)}{1-\left(-2\right)}=\frac{3+3}{1+2}=\frac{6}{3}=2$

Vi set inn koordinatane til eitt av dei oppgitte punkta og verdien for stigingstalet i eittpunktsformelen. Vi kan velje kva punkt vi vil berre det ligg på linja. Her har vi vald punktet $$ \left(1, 3\right)$$.

$\begin{array}{rcl}y-y_1 & = & a\left(x-x_1\right)\\ & & \\ y-3 & =& 2\left(x-1\right)\\ & & \\ y-3 & =& 2x-2\\ & & \\ y & =& 2x+1\end{array}$

Vi har funne likninga for linja.

Alternativ 2. Vi brukar at generell likning for ei rett linje er $\mathrm{y}=\mathrm{ax}+\mathrm{b}$

$y=ax+b$

Sidan punkta $\left(-2, -3\right)$ og $\left(1, 3\right)$ ligg på linja, må koordinatane til desse punkta passe i den generelle likninga $y=ax+b$.

Vi får eit likningssett med to ukjende, $a$ og $b$

$\begin{array}{rcl}-3& =& a·\left(-2\right)+b\end{array}$ og $\begin{array}{rcl}3& =& a·1+b\end{array}$

Startar med den første likninga

$\begin{array}{rcl}-3& = & -2a+b\\ & & \\ b& =& -3+2a\end{array}$

Set dette inn i den andre likninga

$\begin{array}{rcl}3& = & a·1+\left(-3+2a\right)\\ & & \\ 3& =& a-3+2a\\ & & \\ 3a& =& 6\\ & & \\ a& =& 2\end{array}$

Set resultatet for $a$ inn i likninga for $b$

$\begin{array}{rcl}b& = & -3+2·2\\ & & \\ b& =& 1\end{array}$

Likninga for linja blir $y=2x+1$.

Alternativ 3. Grafisk løysing

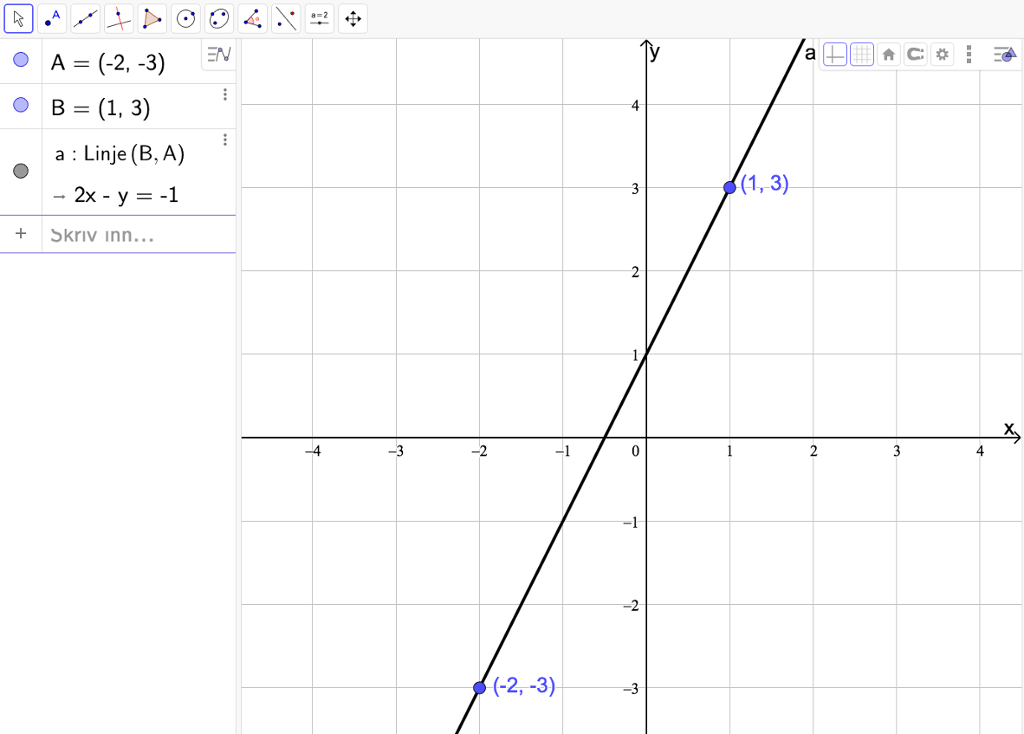
I GeoGebra markerer du punkta $\left(-2, -3\right)$ og $\left(1, 3\right)$ ved å klikke på knappen «Nytt punkt» eller ved å skrive inn punkta på skrivelinja. Klikk så på knappen «Linje» og deretter på dei to punkta. Likninga for linja blir så vist i algebrafeltet

I algebrafeltet på biletet er det vist likninga for linja på ei litt uvand form. Høgreklikk då på likninga for linja og vel at likninga skal visast på formen $y=ax+b$.

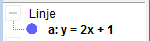
Du får at likninga for linja er $y=2x+1$.

Utan å bruke digitale hjelpemiddel kan du avsetje dei kjente punkta i eit koordinatsystem. Trekk ei rett linje gjennom punkta. Les av kor linja skjer $y$-aksen. Du har då funne konstantleddet. Stigingstalet kan du finne ved å rekne ut endring i $y$-verdi dividert med endring i $x$-verdi.