Stigingstal og konstantledd
Start med å lage to «glidarar», og , i GeoGebra, ved å skrive "" og "" i innskrivingsfeltet.
Skriv så inn . Hugs å skrive gangeteiknet. Då skal du få ei rett linje i grafikkfeltet slik som på biletet nedanfor.
Kva fortel og om grafen til ein lineær funksjon?
Du kan no endre på verdiane til glidarane og samtidig sjå korleis den rette linja endrer seg.
Ser du nokre samanhengar mellom grafane og verdiane til og ?
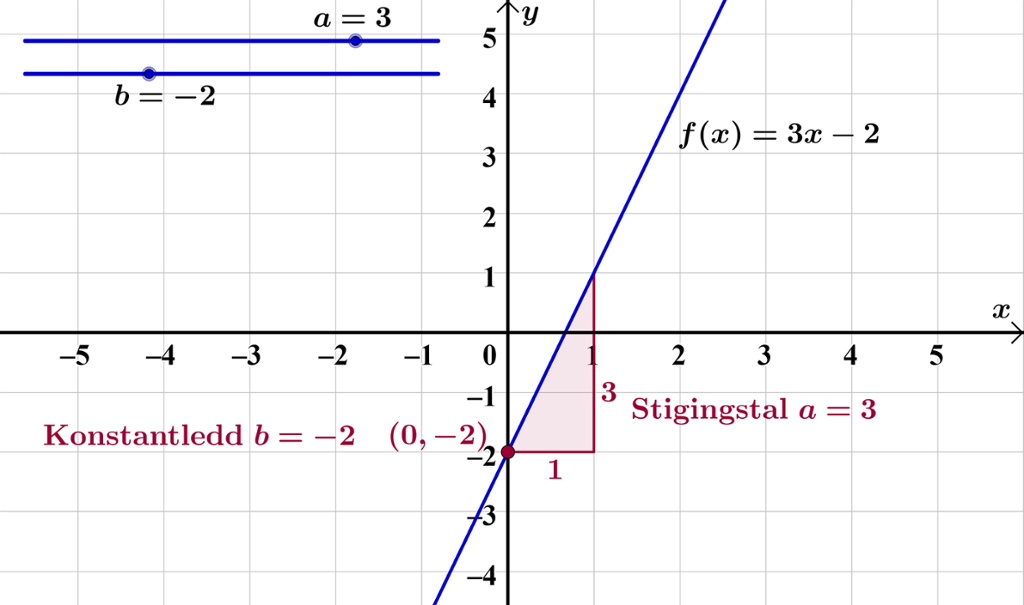
På biletet har vi teikna grafen av for og
. Det tyder at .
Ser du at grafen skjer -aksen der ? Grafen skjer andreaksen når og
.
Talet blir kalla konstantleddet.
Talet viser kor mye grafen stig eller søkk når aukar med eining.
Talet blir kalla stigingstalet.
Dersom stigingstalet er negativt, søkk grafen når aukar.
Nedanfor har vi laga GeoGebra-arket du vart beden om å lage øverst i teksten interaktivt, slik at du kan dra i glidarane for og og sjå korleis den rette linja endrar seg.
Prøv sjølv!
Dra i glidarane for og . Observer kva som skjer.
Oppgåve
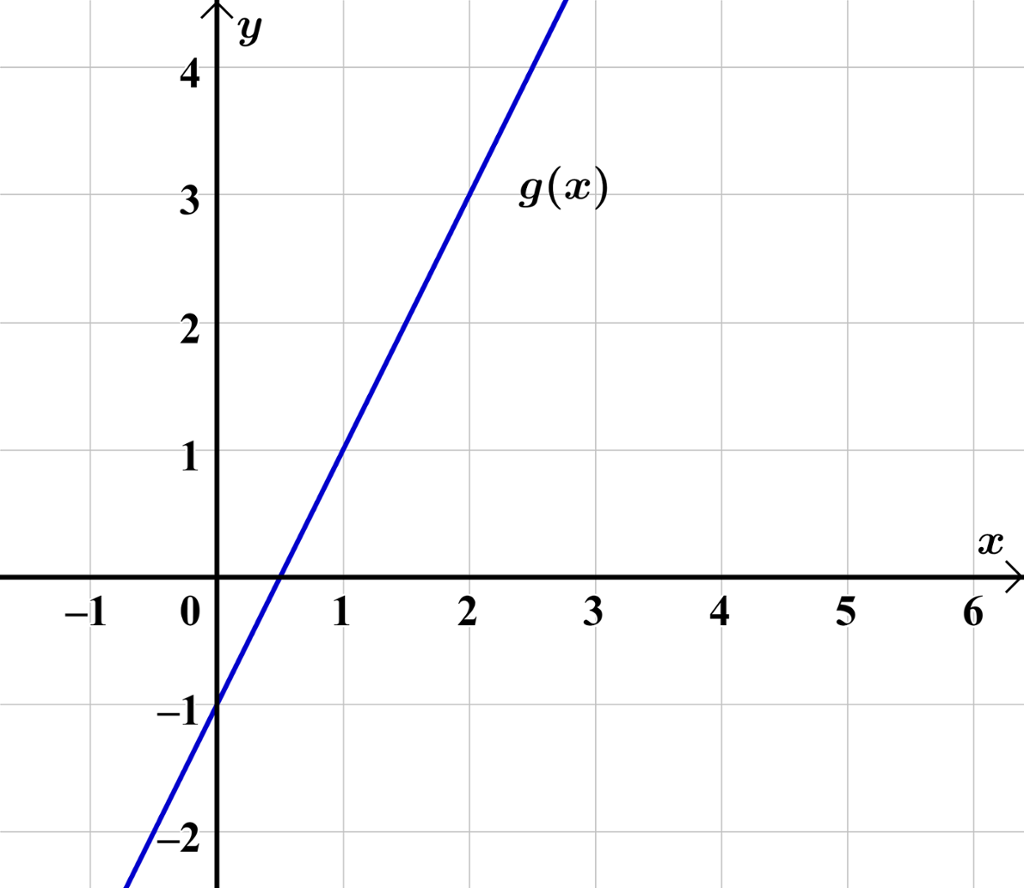
Finn funksjonsuttrykket til den lineære funksjonen på biletet ved å finne stigingstal og konstantledd.
Spesialtilfelle
Du bør merkje deg to spesialtilfelle av lineære funksjonar.
Det eine er når . Då er , og og er proporsjonale storleikar. Talet blir i dette tilfellet kalla proporsjonalitetskonstanten.
Det andre spesialtilfellet er når . Då er og grafen er parallell med -aksen.
Stigingstalet, , seier noko om kor bratt grafen til den lineære funksjonen er.
Konstantleddet,
