Avstand punkt–linje. Vektorfunksjoner
Med avstanden fra et punkt til ei rett linje
Prøv selv
Du kan dra i punktet
Fiillat
Hvor stor er vinkelen mellom linja og linjestykket
Vi skal her vise to metoder for å finne denne avstanden. Det er viktig at du lærer deg begge metodene fordi dette er generelle metoder som kan brukes på andre problemstillinger.
Vi skal bruke en trekant slik som på figuren til hjelp.
Tenk over
Hvordan kan en slik trekant hjelpe oss med å finne avstanden fra et punkt til ei linje?
Vi setter opp to ulike måter for å finne arealet av en trekant slik at vi får en likning der vi kan bestemme
Vi kan regne ut arealet ved hjelp av den vanlige arealformelen for trekanter:
A △ = 1 2 g · h = 1 2 a → · h Vi kan bruke arealformelen som inneholder vektorproduktet mellom
a → b → A △ = 1 2 a → × b →
Disse to formlene må gi samme areal. Vi får
Eksempel
Vi har gitt punktene
Løsning uten hjelpemidler
Vi begynner med å finne
Vi får
Avstanden fra
Løsning med hjelpemidler
Med CAS går dette raskere:
Kontroller at dette er samme svar som vi fikk uten hjelpemidler.
Er det vanskelig å huske formelen for avstanden
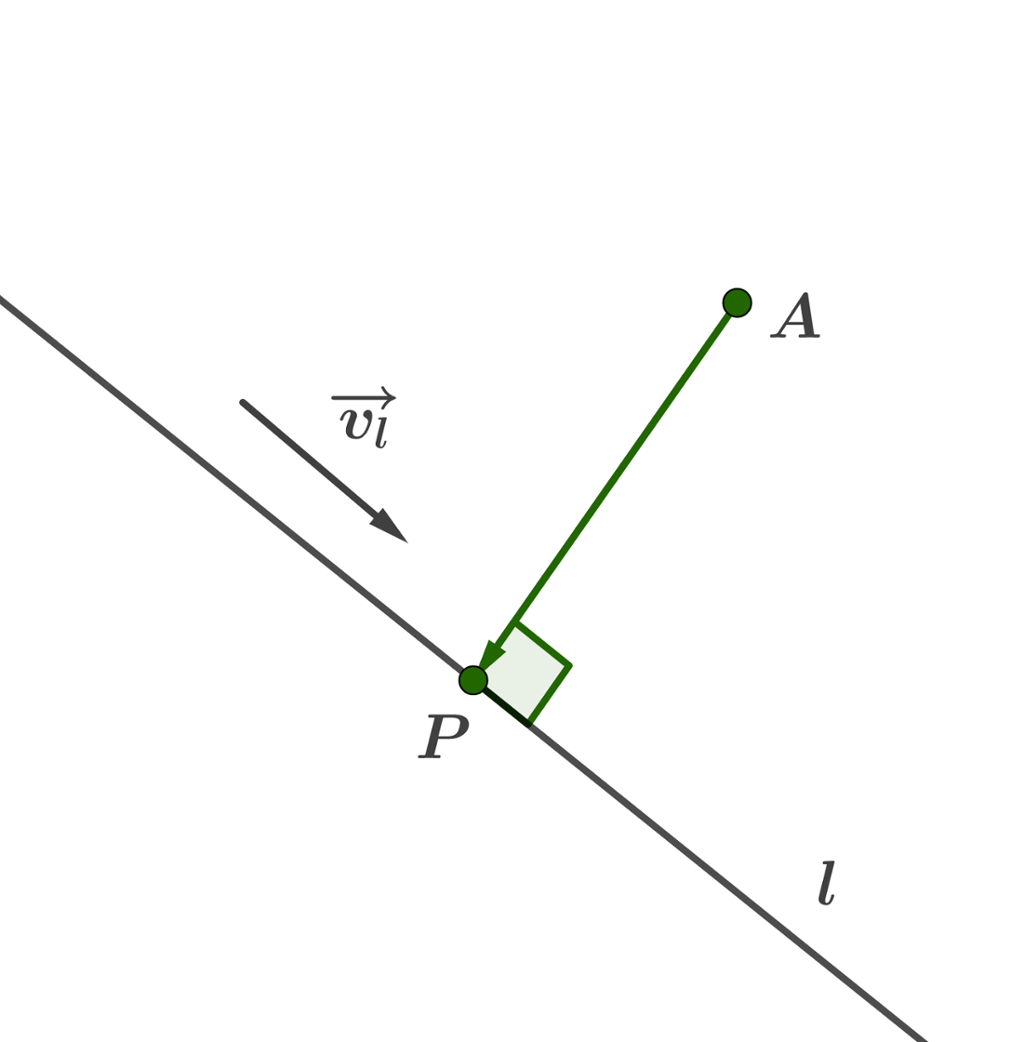
I den andre metoden bruker vi følgende framgangsmåte:
- Vi finner et uttrykk for vektoren fra punktet
A P ( x , y , z ) l - Vi finner deretter den verdien av parameteren som gjør at denne vektoren står vinkelrett på
l A P → · v → l = 0 v → l
retningsvektor for linjal Lengden av den vektoren vi da får, er avstanden fra
A l
Vi velger å vise framgangsmåten med et eksempel.
Eksempel
Gitt ei linje på parameterform
Finn avstanden fra punktet
Løsning uten hjelpemidler
Et vilkårlig punkt
Videre får vi at
For at lengden av
Dette gir videre
Vi setter denne
Avstanden fra
Avstanden fra punktet
Løsning med hjelpemidler
Legg merke til i framgangsmåten med CAS nedenfor at vi skriver inn linja r(t). Vi gjør tilsvarende med AP(t). Dette er nødvendig for å kunne regne med uttrykkene på en enkel måte.
Vi kan også finne en retningsvektor r(t). (Se forklaring lenger ned.)
I linje 4 finner vi en retningsvektor vl for linja ved å derivere r(t). Vi ser at vi får samme retningsvektor som vi brukte da vi løste oppgaven uten hjelpemidler over. I linje 5 løser vi likningen AP(t).
Tenk over
Hvorfor får vi en retningsvektor for linja r(t)?
Når vi skriver linja r(t):=(4-t,5t,2-t) slik vi har gjort det i linje 1 i CAS-bildet over, kaller vi r(t) for en vektorfunksjon. Vi ser på vektoren som en funksjon av variabelen
Tenk over
Er AP(t) i linje 3 en vektorfunksjon?
Vektorfunksjoner og kurver
Når vi skal regne med linjer og kurver i CAS i GeoGebra som i eksempelet her, bør vi skrive dem inn som vektorfunksjoner slik vi har gjort. Dersom vi bare ønsker å tegne en kurve, eller deler av den, bruker vi kommandoen "Kurve".
I eksempelet i metode 1 (arealmetoden) hadde vi oppgitt tre punkter. Da er det som regel enklest å bruke denne metoden. I eksempelet i metode 2 (skalarproduktmetoden) der vi har oppgitt parameterframstillingen av linja, er det som regel enklest å bruke metode 2.