Fágaartihkal

Modeller av figurer og mønster

Figurer og mønster kan vi ofte lage matematiske modeller av.

Figurene ovenfor er bygd opp av 9, 12 og 15 små kvadrater. Tenk deg at vi fortsetter å lage figurer etter samme mønster.

Antall små kvadrater i hver figur danner en serie med tall, en tallfølge, som begynner med tallene 9, 12 og 15 og fortsetter etter samme mønster i det uendelige 9, 12, 15, ...
La $F_{n}$ være antall små kvadrater i figur nummer $n$ slik at $F_{1} = 9, F_{2} = 12$ og $F_{3} = 15$

Prøv å svare på følgende spørsmål før du ser på løsningen.

Hva gjør vi for å komme fra en figur til den neste? Hva er mønsteret i det vi gjør?
Hvor mange små kvadrater vil det være i Figur 4, Figur 5 og Figur 6? Det vil si $F_{4}, F_{5}$ og $F_{6}$ .
Kan du finne en modell, en formel, for antall kvadrater i figur nummer $n$ ? En formel for $F_{n}$ .
Hvor mange kvadrater er det etter din modell i figur nummer 998?

Løsning

Vis løsning

Vi legger til tre små kvadrater for å komme fra én figur til neste.
Figur 4 vil derfor bestå av 18 små kvadrater, Figur 5 av 21 kvadrater og Figur 6 av 24 kvadrater. Det vil si at $F_{4} = 18, F_{5} = 21$ og $F_{6} = 24$ .
Jeg ser at antall kvadrater alltid er lik 3 multiplisert med et tall som er 2 høyere enn «figurnummeret». $F_{1} = 9 = 3 (1 + 2), F_{2} = 12 = 3 (2 + 2)$ , $F_{3} = 15 = 3 (3 + 2), F_{4} = 18 = 3 (4 + 2)$ , $F_{5} = 21 = 3 (5 + 2), F_{6} = 3 (6 + 2)$
Vi får da modellen $F_{n} = 3 (n + 2)$
Antall kvadrater i figur nummer 998 er da $F_{998} = 3 (998 + 2) = 3 \cdot 1000 = 3000$ .

Trekanter

En likesidet $△ A B C$ har areal lik $T$ . Midtpunktene på sidene i $△ A B C$ er hjørnene i en ny likesidet trekant med areal lik $T_{1}$ . Midtpunktene på sidene i $△ D E C$ er hjørnene i en ny likesidet trekant $△ I H G$ med areal lik $T_{2}$ . Etter samme mønster lager vi trekanter med areal $T_{3}$ , $T_{4}$ , og så videre.
Denne prosessen tenker vi oss fortsetter i det uendelige. Se skissen nedenfor.

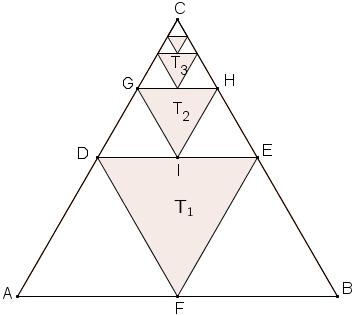
Oppgave

Hva blir arealet til trekant $T_{1}$ ? Hva blir arealet til trekant $T_{2}$ ? Hva blir arealet til trekant $T_{3}$ ?
Kan du finne en modell, en formel, for arealet $T_{n}$ når vi fortsetter å lage trekanter etter samme mønster?
Bruk modellen, og sett opp et uttrykk for arealet $T_{10}$ ? Hva blir arealet $T_{1000}$ ?
Studer figuren og finn ut hva som blir summen av arealene $T_{1}, T_{2}, T_{3}$ , og så videre. Omkretsen av $△ A B C$ er lik 3. Trekanten som har areal lik $T_{n}$ har omkrets $O_{n}$ .
Forklar at $O_{1} = \frac{3}{2}, O_{2} = \frac{3}{4} og O_{3} = \frac{3}{8}$ .
Kan du finne en modell, en formel, for omkretsen til trekant nr. $n$ når vi fortsetter å lage trekanter etter samme mønster?
Bruk modellen og finn $O_{4}$ .

Løsning

Vis løsning

$△ F E D$ er én av fire like store likesidede trekanter med samlet areal lik arealet til $△ A B C$ . $△ F E D$ har derfor arealet $T_{1} = \frac{T}{4^{1}}$ . $△ I H G$ er én av fire like store likesidede trekanter med samlet areal lik arealet til $△ D E C$ . $△ I H G$ har derfor arealet $T_{2} = \frac{T}{4} \cdot \frac{1}{4} = \frac{T}{4^{2}}$ .
Tilsvarende er $T_{3} = T_{2} \cdot \frac{1}{4} = \frac{T}{4^{2}} \cdot \frac{1}{4} = \frac{T}{4^{3}}$ , og slik fortsetter det.
Det betyr at vi får modellen for arealet $T_{n} = \frac{T}{4^{n}}$ .
Vi bruker modellen og får at $T_{10} = \frac{T}{4^{10}} og T_{1000} = \frac{T}{4^{1000}}$ .
$T_{1}$ utgjør tredjeparten av arealet til firkanten $A B E D$ , $T_{2}$ utgjør tredjeparten av arealet til firkanten $D E H G$ , og slik fortsetter det.
Det må bety at summen av alle de fargelagte trekantene må være lik tredjedelen av arealet til den store trekanten. Vi kan skrive det slik $T_{1} + T_{2} + T_{3} + . . . = \frac{T}{3}$ .
Sidene i $△ F E D$ er halvparten av sidene i $△ A B C$ . Omkretsen til $△ F E D$ må da være halvparten av omkretsen til $△ A B C$ . Det vil si at $O_{1} = \frac{3}{2^{1}}$ . Sidene i $△ I H G$ er halvparten av sidene i $△ F E D$ . Omkretsen til $△ I H G$ må da være halvparten av omkretsen til $△ F E D$ . Det vil si at $O_{2} = O_{1} \cdot \frac{1}{2} = \frac{3}{2} \cdot \frac{1}{2} = \frac{3}{2^{2}}$ .
Tilsvarende er $O_{3} = O_{2} \cdot \frac{1}{2} = \frac{3}{2^{2}} \cdot \frac{1}{2} = \frac{3}{2^{3}}$ , og slik fortsetter det.
Det betyr at vi får modellen for omkretsen, $O_{n} = \frac{3}{2^{n}}$ .
Vi bruker modellen og får at $O_{4} = \frac{3}{2^{4}} = \frac{3}{16}$ .

Trekanter

Njuolggadusat teavstta geavaheapmái "Modeller av figurer og mønster"