Praktiske eksempler med eksponentialfunksjoner

Hvis du setter kr i banken i dag og får rente på pengene, kan du om ett år ta ut kroner
Etter to år kan du ta ut
Etter tre år kan du ta ut
Etter år kan du ta ut .
Tallet kaller vi for vekstfaktoren.
Innestående beløp, , er en funksjon av antall år i banken, , og funksjonsuttrykket blir
Funksjonen kalles en eksponentialfunksjon siden den variable opptrer som eksponent i en potens.
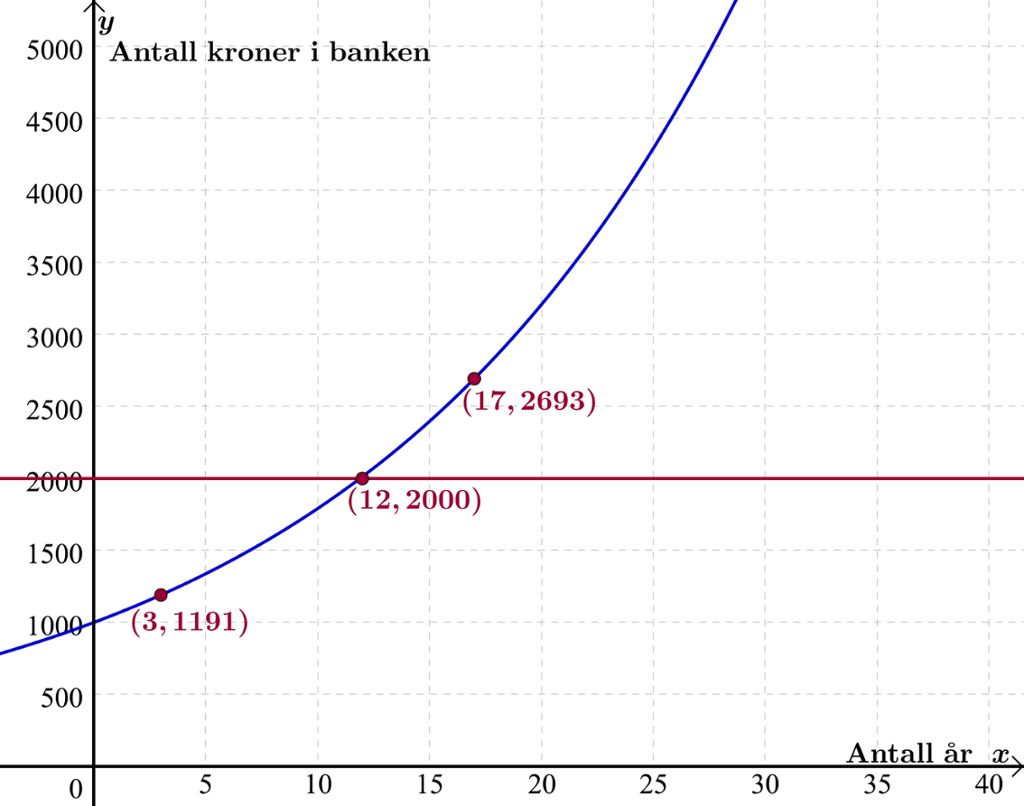
Grafen til funksjonen viser for eksempel at beløpet på kroner har vokst til kroner etter år og til kroner etter år.
Hvor lenge må pengene stå i banken før beløpet er fordoblet?
Vi finner svaret ved å tegne den rette linja i samme koordinatsystem som grafen til og så finne skjæringspunktet mellom linja og grafen. Pengene må stå i banken i år.
Dette kan vi også finne ved regning.
Vi setter antall år pengene må stå i banken lik og får likningen
Dette er en eksponentiallikning.
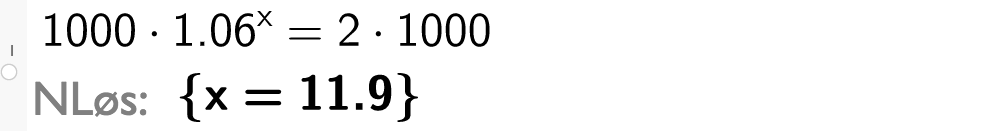
Denne likningen løser vi ved CAS i GeoGebra

Kari kjøper en fire år gammel bil for kroner. Bilen har sunket i verdi med hvert år siden den var ny. Kari regner med at verdien vil synke på samme måte de neste årene.
Verdien på bilen ett år etter at Kari kjøpte den blir kroner
Verdien på bilen år etter at Kari kjøpte den blir kroner
Når har verdien på bilen sunket til halvparten av det Kari betalte for den, og hva kan vi regne med at bilen kostet da den var ny?
Bilens verdi , antall år etter at Kari kjøpte den, er da gitt ved eksponentialfunksjonen
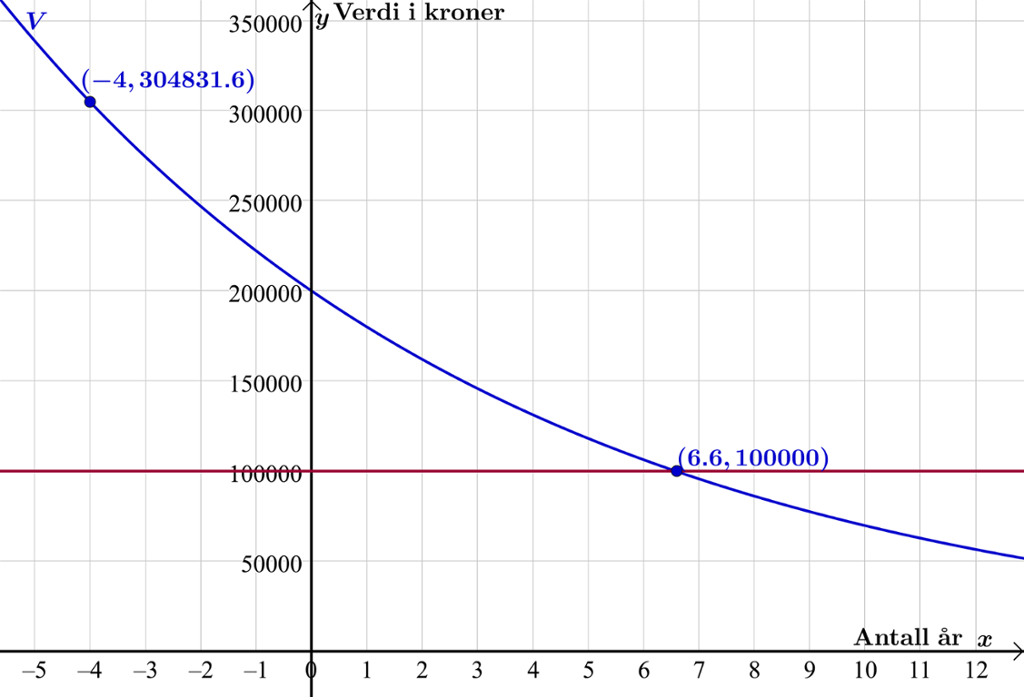
Vi tegner grafen til .
Vi tegner den rette linja og finner skjæringspunktet mellom denne og grafen til . Da ser vi at bilen er verdt 100 000 kroner om cirka seks og et halvt år. Så skriver vi i inntastingsfeltet og får et nytt punkt på grafen til . Da ser vi at bilen kostet omtrent 305 000 kroner da den var ny.
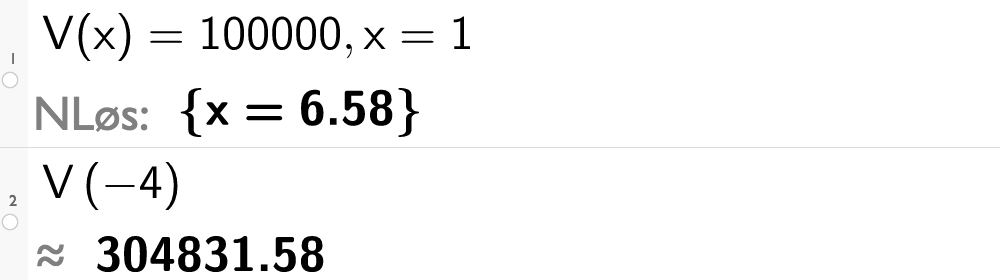
Vi kan finne det samme ved regning. Husk at du ikke trenger definere funksjonen på nytt når den finnes i algebrafeltet.