Fagartikkel

Sinussetninga

Vi skal no bli kjende med ei setning som gjer oss i stand til å finne sidelengder og vinklar i trekantar som ikkje er rettvinkla.

Gitt ein trekant $A B C$ . Følgjande setning gjeld

Trekant med hjørne stor a, stor b og stor c og sider liten a, liten b og liten c slik at sida liten a er motståande side til hjørnet stor a, og tilsvarande. Illustrasjon. — Bilete: Olav Kristensen, Stein Aanensen / CC BY-NC-SA 4.0

Sinussetninga

$\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}$

Forholdet mellom sinus til ein vinkel og lengda av motståande side er lik for alle vinklane i trekanten.

Prov for sinussetninga

Trekant med hjørner stor a, stor b og stor c og sider liten a, liten b og liten c slik at siden liten a er motstående side til hjørnet stor a, og tilsvarende. Illustrasjon. — Bilete: Olav Kristensen, Stein Aanensen / CC BY-NC-SA 4.0

Vi skal no prove sinussetninga ved å skrive opp formelen for arealet av $Δ A B C$ ut frå kvar av dei tre vinklane.

Sett frå hjørnet $A$ blir arealet av $Δ A B C$ lik $\frac{1}{2} \cdot b \cdot c \cdot \sin A$ .
Sett frå hjørnet $B$ blir arealet av $Δ A B C$ lik $\frac{1}{2} \cdot a \cdot c \cdot \sin B$ .
Sett frå hjørnet $C$ blir arealet av $Δ A B C$ lik $\frac{1}{2} \cdot a \cdot b \cdot \sin C$ .

Desse areala MÅ jo vere like store, og vi set

$\begin{array}{rcl} \frac{1}{2} \cdot b \cdot c \cdot \sin A & = & \frac{1}{2} \cdot a \cdot c \cdot \sin B = \frac{1}{2} \cdot a \cdot b \cdot \sin C \\ 2 \cdot \frac{1}{2} \cdot b \cdot c \cdot \sin A & = & 2 \cdot \frac{1}{2} \cdot a \cdot c \cdot \sin B = 2 \cdot \frac{1}{2} \cdot a \cdot b \cdot \sin C \\ b \cdot c \cdot \sin A & = & a \cdot c \cdot \sin B = a \cdot b \cdot \sin C \\ \frac{b \cdot c \cdot \sin A}{a \cdot b \cdot c} & = & \frac{a \cdot c \cdot \sin B}{a \cdot b \cdot c} = \frac{a \cdot b \cdot \sin C}{a \cdot b \cdot c} \\ \frac{b \cdot c \cdot \sin A}{a \cdot b \cdot c} & = & \frac{a \cdot c \cdot \sin B}{a \cdot b \cdot c} = \frac{a \cdot b \cdot \sin C}{a \cdot b \cdot c} \\ \frac{\sin A}{a} & = & \frac{\sin B}{b} = \frac{\sin C}{c} \end{array}$

Dette må gjelde for alle trekantar!

Eksempel

Figuren viser ein trekant $A B C$ .

HJeplefigur — Bilete: Olav Kristensen, Stein Aanensen / CC BY-SA 4.0

Rekn ut $∠ A$ når $a = 3, 0 cm, b = 5, 5 cm$ og $∠ B = 60 °$ .
Løysing
Bilete: GeoGebra / CC BY-NC-SA 4.0

Med $∠ A = 151, 8 °$ blir vinkelsummen i trekanten større enn $180 °$ fordi $151, 8 ° + 60 ° = 211, 8 °$ . Vi får då ikkje nokon trekant. Løysinga $∠ A = 151, 8 °$ kan difor ikkje brukast. $∠ A = 28, 2 °$
Finn sida $c$ .>/p>
Løysing
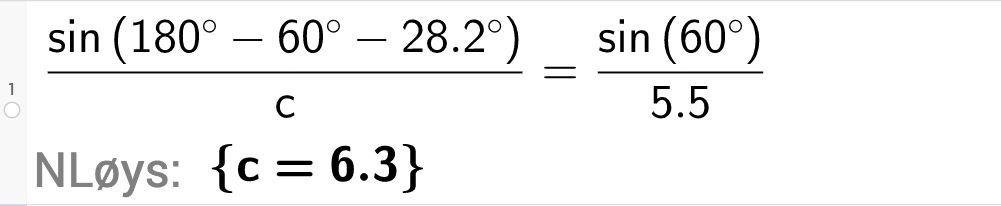$sinus til 180 gradar minus 60 gradar minus 28 komma 2 gradar delt på c \$
Bilete: GeoGebra / CC BY-NC-SA 4.0
$c = 6, 3 cm$

Legg merke til:

Når vi finn vinklar med sinussetninga, fører rekninga til to mogelege verdiar for vinkelen.

I kvar enkelt oppgåve må vi vurdere om begge svara kan brukast.

Vi utelukkar eventuelt vinklar ved å bruke at

Vinkelsummen i ein trekant skal vere $180 °$
Den største vinkelen skal ha lengst motståande side
Den minste vinkelen skal ha kortast motståande side

Sinussetninga

Prov for sinussetninga

Eksempel

Løysing

Løysing

Reglar for bruk av teksten "Sinussetninga"