Forkort brøkane.
a) x 2 - 25 x + 5
Løysing x 2 - 25 x + 5 = x + 5 x - 5 x + 5 = x - 5
b) x 2 - 81 3 x + 27
Løysing x 2 - 81 3 x + 27 = x + 9 x - 9 3 x + 9 = x - 9 3
c) 16 x 2 - 64 4 x + 8
Løysing 16 x 2 - 64 4 x + 8 = 16 x 2 - 4 4 x + 2 = 4 · 4 x + 2 x - 2 4 x + 2 = 4 x - 8
d) 100 x 2 - 1 10 x - 1
Løysing 100 x 2 - 1 10 x - 1 = 10 x + 1 10 x - 1 10 x - 1 = 10 x + 1
e) 2 a 2 - 50 18 a - 90
Løysing 2 a 2 - 50 18 a - 90 = 2 a 2 - 25 18 a - 5 = 2 a 2 - 5 2 2 · 9 a - 5 = 2 a - 5 a + 5 2 · 9 a - 5 = a + 5 9
f) 2 x 2 - 8 x - 2
Løysing 2 x 2 - 8 x - 2 = 2 x 2 - 2 2 x - 2 = 2 x - 2 x + 2 x - 2 = 2 x + 4
Forkort brøkane.
a) x 2 - 1 4 2 x - 1
Løysing x 2 - 1 4 2 x - 1 = x - 1 2 x + 1 2 2 x - 1 2 = x + 1 2 2 = x 2 + 1 4
b) x 2 - 4 x + 4 x - 2
Løysing x 2 - 4 x + 4 x - 2 = x - 2 x - 2 x - 2 = x - 2
c) 3 x 2 - 18 x + 27 2 x - 6
Løysing 3 x 2 - 18 x + 27 2 x - 6 = 3 x 2 - 6 x + 9 2 x - 3 = 3 x - 3 x - 3 2 x - 3 = 3 x - 3 2
d) x 2 - x + 1 4 2 x - 1
Løysing x 2 - x + 1 4 2 x - 1 = x - 1 2 x - 1 2 2 x - 1 2 = x - 1 2 2 = 2 x - 1 4 = x 2 - 1 4
e) 2 x 2 - 2 9 6 x - 2
Løysing 2 x 2 - 2 9 6 x - 2 = 2 x - 1 3 x + 1 3 2 · 3 x - 1 3 = x + 1 3 3 = 3 x + 1 9 = x 3 + 1 9
Forkort brøkane.
a) 1 - x x - 1
Løysing 1 - x x - 1 = - - 1 + x x - 1 = - x - 1 x - 1 = - 1
b) 1 - x 2 x 2 - 1
Løysing 1 - x 2 x 2 - 1 = - - 1 + x 2 x 2 - 1 = - 1
c) 1 - x x 2 - 1
Løysing 1 - x x 2 - 1 = - - 1 + x x - 1 x + 1 = - 1 x + 1
d) x - 1 2 + 2 x - 1 2 x 2 - 2
Løysing Her kan vi setje x - 1
x - 1 2 + 2 x - 1 2 x 2 - 2 = x - 1 x - 1 + 2 2 x 2 - 1 = x - 1 x + 1 2 x - 1 x + 1 = 1 2
Trekk saman og forkort.
a) 2 x - 1 - 1 x + 1
Løysing = 2 x + 1 x - 1 x + 1 - 1 x - 1 x + 1 x - 1 = 2 x + 2 - x - 1 x - 1 x + 1 = 2 x + 2 - x + 1 x - 1 x + 1 = x + 3 x - 1 x + 1
b) 4 2 x - 1 - 8 4 x 2 - 1
Løysing = 4 2 x + 1 2 x - 1 2 x + 1 - 8 2 x - 1 2 x + 1 = 8 x + 4 - 8 2 x - 1 2 x + 1 = 8 x - 4 2 x - 1 2 x + 1 = 4 2 x - 1 2 x - 1 2 x + 1 = 4 2 x + 1
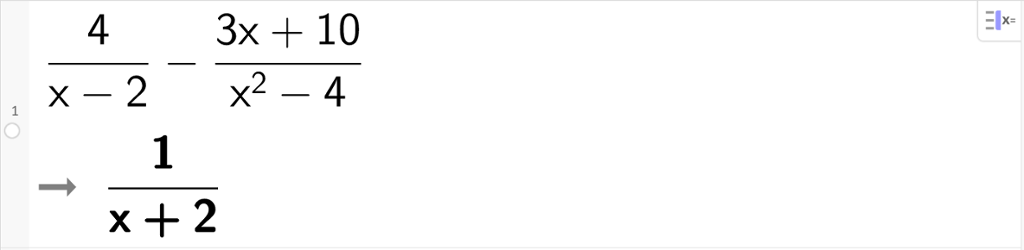
c) 4 x - 2 - 3 x + 10 x 2 - 4
Løysing = 4 x + 2 x - 2 x + 2 - 3 x + 10 x - 2 x + 2 = 4 x + 8 - 3 x - 10 x - 2 x + 2 = x - 2 x - 2 x + 2 = 1 x + 2
d) 4 2 x - 10 - 3 x 2 + 15 2 x 2 - 25
Løysing = 4 2 x - 5 - 3 x · 2 2 + 15 · 2 2 2 x - 5 x + 5 = 4 2 x - 5 - 3 x + 5 2 x - 5 x + 5 = 4 - 3 2 x - 5 = 1 2 x - 5
a) Løys oppgåve 4 c) digitalt.
Løysing b) Løys oppgåve 4 d) digitalt.
Løysing Her kan vi bruke knappen for faktorisering etterpå (sjå linje 2 i CAS-biletet nedanfor) for å få det forenkla uttrykket på same form som i oppgåve 1.5.11 b).
Forenkling og faktorisering med CAS.
Rekn ut og forkort.
a) x 2 + 6 x + 9 x - 2 · x 2 - 4 x 2 + 2 x - 3
Løysing x 2 + 6 x + 9 x - 2 · x 2 - 4 x 2 + 2 x - 3 = x + 3 x + 3 x - 2 · x + 2 x - 2 x + 3 x - 1 = x + 3 x + 3 x + 2 x - 2 x - 2 x + 3 x - 1 = x 2 + 5 x + 6 x - 1
b) x 2 + 2 x - 8 x 2 - 16 : x 2 - 4 x 2 - 2 x - 8
Løysing x 2 + 2 x - 8 x 2 - 16 : x 2 - 4 x 2 - 2 x - 8 = x 2 + 2 x - 8 x 2 - 16 · x 2 - 2 x - 8 x 2 - 4 = x + 4 x - 2 x - 4 x + 2 x + 4 x - 4 x + 2 x - 2 = 1
Trekk saman og forkort.
a) 1 x + 2 - 3 x - 2 + 6 x x 2 - 4
Løysing 1 x + 2 - 3 x - 2 + 6 x x 2 - 4 = 1 x + 2 - 3 x - 2 + 6 x x + 2 x - 2 = 1 · x - 2 x + 2 · x - 2 - 3 · x + 2 x - 2 · x + 2 + 6 x x + 2 x - 2 = x - 2 - 3 ( x + 2 ) + 6 x x + 2 · x - 2 = 4 x - 8 x + 2 · x - 2 = 4 x - 2 x + 2 · x - 2 = 4 x + 2
b) 2 x 2 x - 2 - 2 2 ( x + 1 ) + 2 x x 2 - 1
Løysing 2 x 2 x - 2 - 2 2 ( x + 1 ) + 2 x x 2 - 1 = 2 x 2 x - 1 - 2 2 ( x + 1 ) + 2 x x + 1 x - 1 = 2 x · x + 1 2 x - 1 · x + 1 - 2 · x - 1 2 ( x + 1 ) · x - 1 + 2 x · 2 x + 1 x - 1 · 2 = 2 x 2 + 2 x - 2 x + 2 + 4 x 2 · x + 1 · x - 1 = 2 x 2 + 4 x + 2 2 · x + 1 · x - 1 = 2 x 2 + 2 x + 1 2 · x + 1 · x - 1 = 2 x + 1 2 2 · x + 1 · x - 1 = 2 x + 1 x + 1 2 · x + 1 · x - 1 = x + 1 x - 1
c) x x 2 + 4 x + 3 - 2 x 2 - 2 x - 3 + 3 x 2 - 9
Løysing x x 2 + 4 x + 3 - 2 x 2 - 2 x - 3 + 3 x 2 - 9 = x x + 3 x + 1 - 2 x + 1 x - 3 + 3 x + 3 x - 3 = x · x - 3 x + 3 x + 1 · x - 3 - 2 · x + 3 x + 1 x - 3 · x + 3 + 3 · x + 1 x + 3 x - 3 · x + 1 = x · x - 3 - 2 · x + 3 + 3 · x + 1 x + 3 x + 1 · x - 3 = x 2 - 3 x - 2 x - 6 + 3 x + 3 x + 3 x + 1 · x - 3 = x 2 - 2 x - 3 x + 3 x + 1 · x - 3 = x - 3 x + 1 x + 3 x + 1 · x - 3 = 1 x + 3
Trekk saman og forkort.
a) x x - 1 - x - 3 2 x - 2
Løysing x x - 1 - x - 3 2 x - 2 = 2 · x 2 ( x - 1 ) - x - 3 2 x - 1 = 2 x - x + 3 2 x - 1 = x + 3 2 x - 2
b) 2 x - 1 + x x 2 - 3 x + 2
Løysing 2 x - 1 + x x 2 - 3 x + 2 = x - 2 · 2 x - 2 x - 1 + x x - 2 x - 1 = 2 x - 4 + x x - 1 x - 2 = 3 x - 4 x - 1 x - 2
c) x x - 1 + 2 - x x + 3 - x - 2 x 2 + 2 x - 3
Løysing x x - 1 + 2 - x x + 3 - x - 2 x 2 + 2 x - 3 = x + 3 · x x + 3 x - 1 + x - 1 2 - x x - 1 x + 3 - x - 2 x + 3 x - 1 = x 2 + 3 x + 2 x - x 2 - 2 + x - x + 2 x + 3 x - 1 = x 2 + 3 x + 2 x - x 2 - 2 + x - x + 2 x + 3 x - 1 = 5 x x + 3 x - 1
d) 1 2 x - 2 - 2 x - 1 x - 2 + 3 x 2 - 3 x + 2
Løysing 1 2 x - 2 - 2 x - 1 x - 2 + 3 x 2 - 3 x + 2 = x - 2 · 1 x - 2 · 2 x - 1 - 2 x - 1 2 x - 1 2 x - 1 x - 2 + 2 · 3 2 x - 1 x - 2 = x - 2 - 2 2 x 2 - x - 2 x + 1 + 6 2 x - 1 x - 2 = x - 2 - 4 x 2 + 2 x + 4 x - 2 + 6 2 x - 1 x - 2 = - 4 x 2 + 7 x + 2 2 x - 1 x - 2 = - 4 x + 1 4 x - 2 2 x - 1 x - 2 = 4 x + 1 2 x - 1
a) Bestem a
x - a x 2 - 6 x + 8
Løysing Først faktoriserer vi nemnaren.
x 2 - 6 x + 8 = x - 2 x - 4
Skal brøken kunne forkortast, må a
b) Bestem t
2 x - t x 2 - 2 x + 1
Løysing Først faktoriserer vi nemnaren.
x 2 - 2 x + 1 = x - 1 x - 1
Skal brøken kunne forkortast, må anten x + 1 x - 1
2 x - t = 2 x - t 2
Det betyr at vi har:
t 2 = ± 1 t = ± 2
Skal brøken kunne forkortast, må t 2 x - 2 = 2 ( x - 1 )