Korleis bestemme den deriverte i eit punkt algebraisk

I kompetansemåla i R1 står det at du skal kunne bestemme den deriverte i eit punkt algebraisk. Dette har du allereie vore innom i 1T då du jobba med definisjonen til den deriverte. Då brukte du definisjonen til å rekne ut eit uttrykk for den deriverte. Du finn artikkelen som går gjennom det nedst på sida.

Her vil vil ikkje gå vegen om å finne funksjonsuttrykket til den deriverte, men bruke definisjonen direkte til å finne den deriverte i eit punkt.

Vi vil rekne oss fram til den deriverte til funksjonen $f$ gitt ved

$f\left(x\right)=x^2+2x+3$ når $x=0,5$

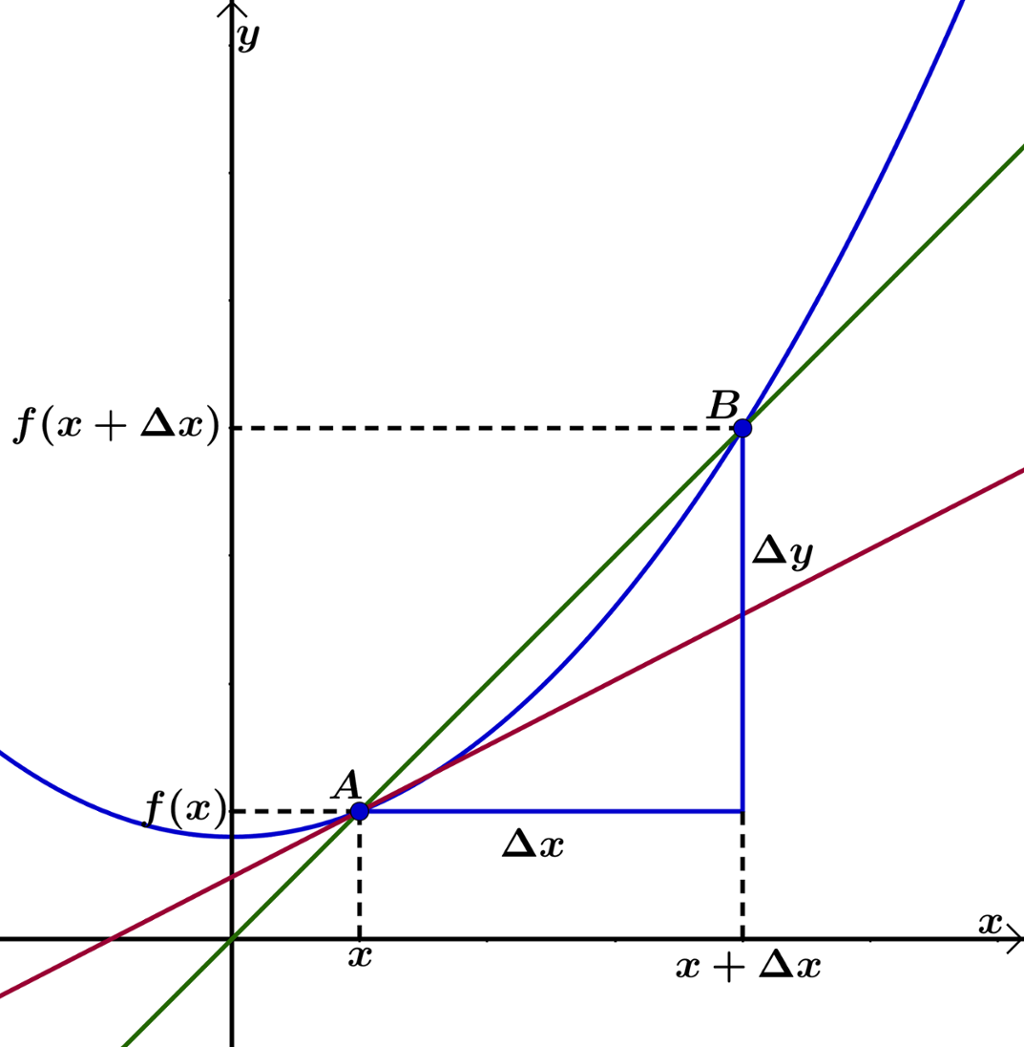
Definisjonen av den deriverte seier at $$ f^{\text{'}}\left(x\right)$$ er den verdien som $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\frac{f\left(x+\mathrm{\Delta }x\right)-f\left(x\right)}{\mathrm{\Delta }x}$ nærmar seg mot når $\mathrm{\Delta }x$ går mot null. Når vi skal finne den deriverte der $$ x=0,5$$, får vi

$$ f^{\text{'}}\left(0,5\right)\begin{array}{cl}=& \underset{\mathrm{\Delta }x\to 0}{\lim }\frac{f\left(0,5+\mathrm{\Delta }x\right)-f\left(0,5\right)}{\mathrm{\Delta }x}\end{array}$$

Det gir

$$ \begin{array}{rcl}{f}^{\text{'}}(0,5)& = & \underset{x\to 0}{\lim }\frac{f(0,5+∆x)-f(0,5)}{∆x}\\ & & \\ & =& \underset{∆x\to 0}{\lim }\frac{(0,5+∆x{)}^2+2(0,5+∆x)+3-(0,5^2+2·0,5+3)}{∆x}\\ & & \\ & =& \underset{∆x\to 0}{\lim }\frac{0,5^2+2·0,5·∆x+(∆x{)}^2+2·0,5+2·∆x+3-0,5^2-2·0,5-3}{∆x}\\ & & \\ & =& \underset{∆x\to 0}{\lim }\frac{∆x+(∆x{)}^2+2·∆x}{∆x}\\ & & \\ & =& \underset{∆x\to 0}{\lim }\frac{∆x(1+∆x+2)}{∆x}\\ & & \\ & =& \underset{∆x\to 0}{\lim }\frac{\cancel{∆x}(1+∆x+2)}{\cancel{∆x}}\\ & & \\ & =& \underset{∆x\to 0}{\lim }\left(1+∆x+2\right)\\ & & \\ & =& 3\end{array}$$

Dette betyr at når $f\left(x\right)=x^2+2x+3$, er $$ f^{\text{'}}\left(0,5\right)=3$$.

Du skal heldigvis sleppe å alltid bruke denne metoden når du deriverer funksjonar algebraisk. I matematikk R1 vil du lære fleire ulike derivasjonsreglar som gjer derivasjonsjobben lettare. Desse ligg i emnet "Derivasjonsreglar og deriverbarheit", som du finn lenkje til rett under her.