Definisjonen av den deriverte
Vi nyttar same prinsipp som vi brukte for å finne ein tilnærma verdi for den momentane vekstfarten.
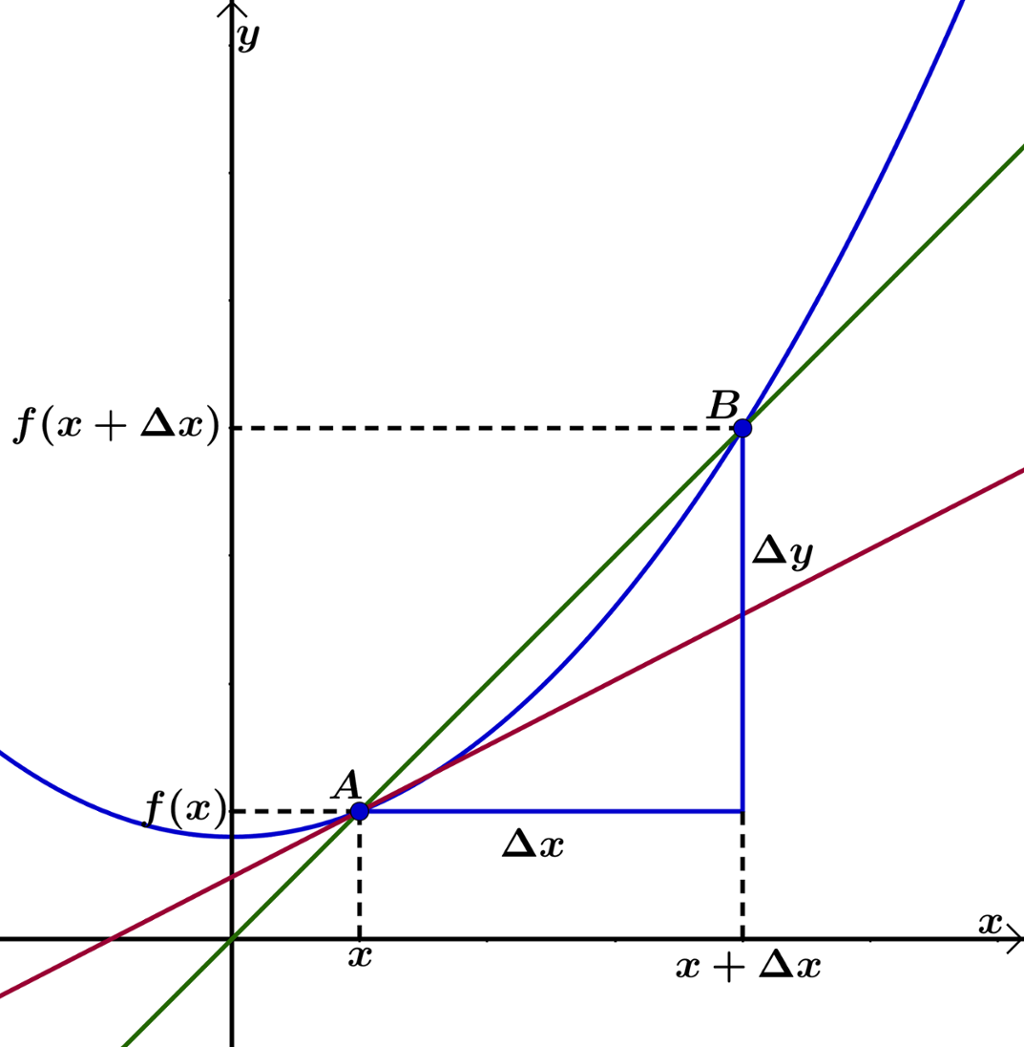
Vi tar utgangspunkt i ein tilfeldig funksjon .
Vi teiknar grafen av funksjonen, vel ein tilfeldig -verdi og får eit punkt på grafen .
Vi ønskjer å finne vekstfarten til funksjonen for akkurat denne -verdien.
Vi gir eit tillegg og får eit nytt punkt på grafen, .
Vi trekkjer ein sekant (grøn linje) gjennom punkta A og B.
Vi reknar ut stigingstalet til denne linja:
Vi har då funne eit uttrykk for gjennomsnittleg vekstfart frå A til B.
Vi lèt no punktet B nærme seg punktet A. Vi lèt altså gå mot null.
Då vil sekanten (grøn) gradvis nærme seg til å bli ein tangent (raud linje) til kurva i A.
Stigingstalet (brattleiken) til denne tangenten fortel kor fort kurva veks akkurat her. Vi kallar dette stigingstalet for den momentane veksten i punktet eller den deriverte av i punktet. Vi skriv og les «
Legg merke til at teiknet for den deriverte er ein liten apostrof.
Den deriverte
Vi ser på grafen ovanfor.
nærmar seg mot når
Den deriverte i eit punkt er stigingstalet til tangenten til grafen i dette punktet.
Den deriverte i eit punkt og den momentane vekstfarten i punktet er det same.
Definisjonen av den deriverte er ein lokal definisjon. Han seier noko om verdien av den deriverte i eit punkt, nemleg punktet med førstekoordinaten
Derivere tyder "å utleie eller avleie" og
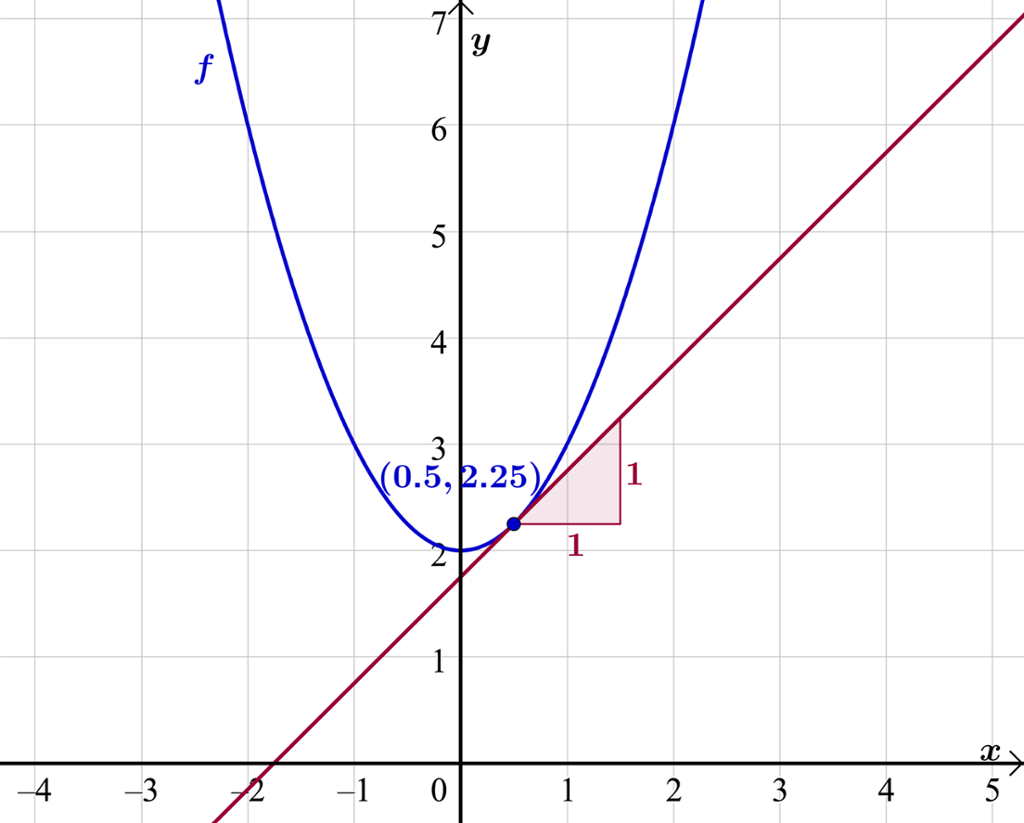
Den momentane vekstfarten eller den deriverte av
Vi kan finne ein verdi for denne vekstfarten grafisk ved å teikne grafen av
Vi ser at tangenten har stigingstalet
Den deriverte av f(x) når
Vi vil no rekne oss fram til den deriverte av
Vi hugsar definisjonen på den deriverte
Korleis finn vi så
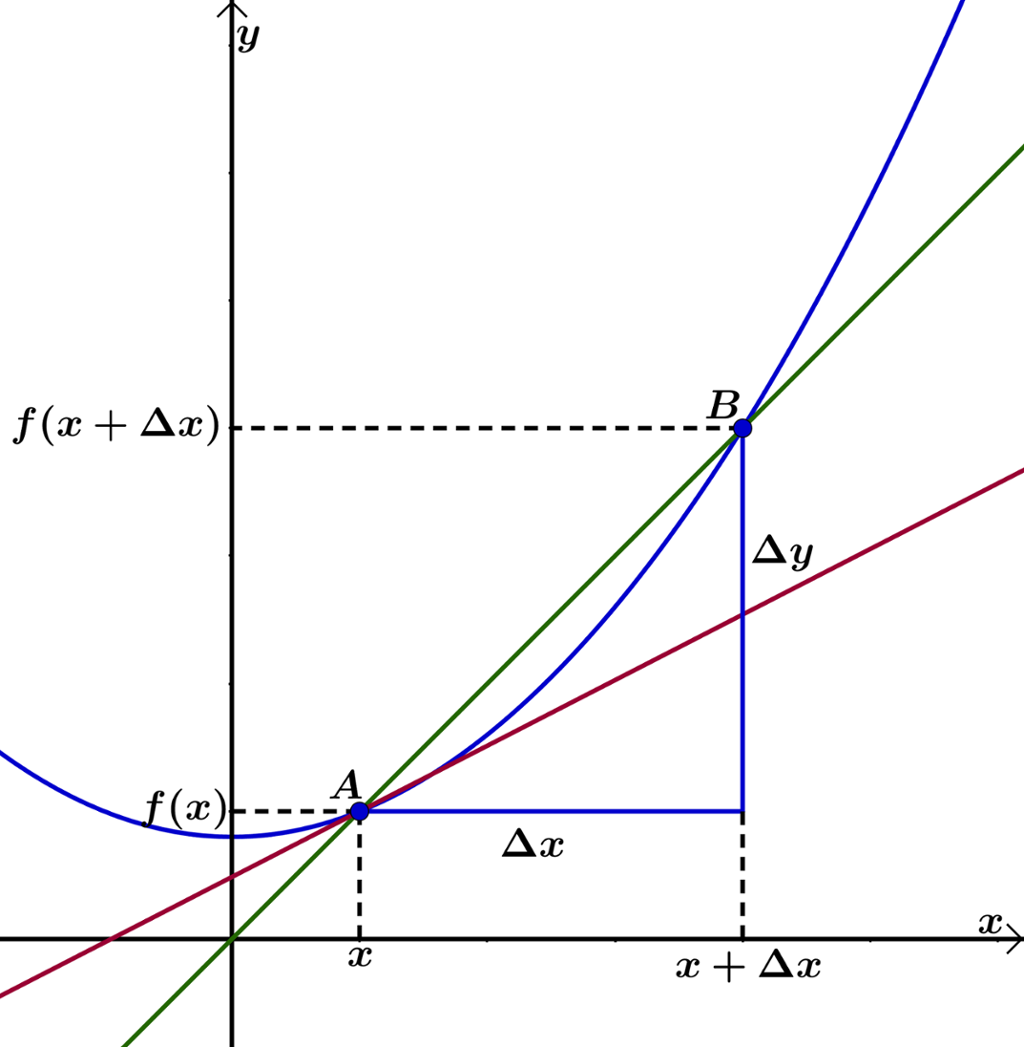
Det gir
(Hugs at
Når
Vi har no funne at når
Då kan vi rekne ut
Den deriverte funksjonen av
Vi kan bruke denne funksjonen til å finne den momentane vekstfarten for alle verdiar av
Til dømes er