Trekanttall og Pascals talltrekant
Følgende figurer er kommet fram ved å lage likesida trekanter av sirkler som er tettpakka.
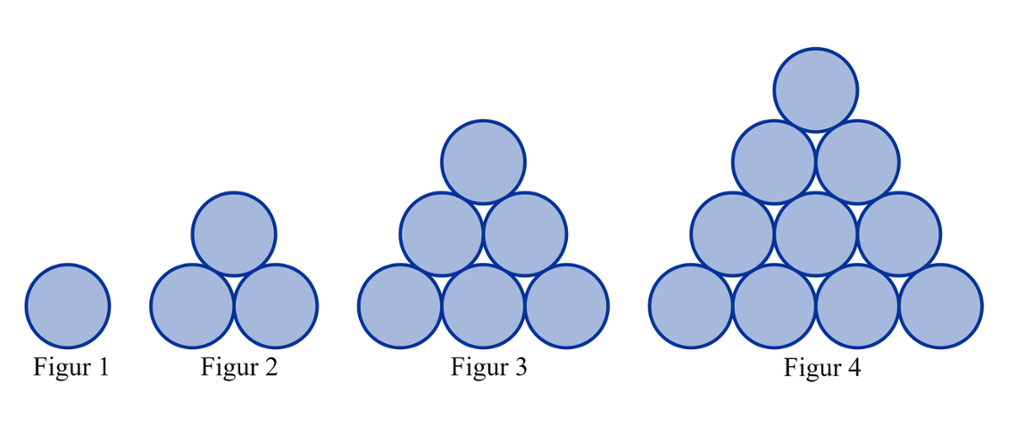
Kan du se hva som er mønsteret i oppbyggingen av figurene?
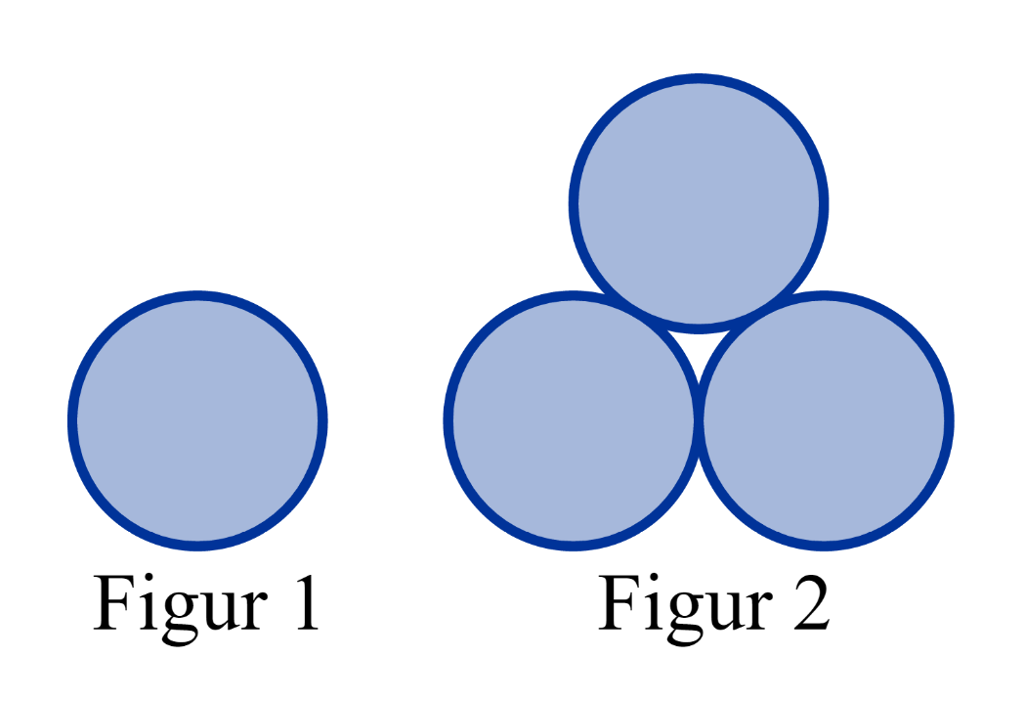
Start med figur 1 og figur 2 nedenfor og ikke se på figur 3 og figur 4 ovenfor.
Klarer du selv å lage figur 3 og figur 4?
Du har kanskje allerede sett mønsteret. Figur 1 har 1 sirkel. Figur 2 har 2 sirkler fler enn figur 1. Figur 3 har 3 sirkler fler enn figur 2. Slik fortsetter det.
Vi får da at i figur 1 er det 1 sirkel. I figur 2 er det sirkler. I figur 3 er det
sirkler. I figur 4 er det sirkler og så videre.
Tallene 1, 3, 6, 10 og så videre kalles for trekanttallene. Hvorfor tror du de har fått dette navnet?
La være trekanttall nummer . Da er
og .
Tenk nå at vi lager figur 5, figur 6 og så videre etter samme mønster. Ser du at
og ?
Ser du at vi generelt får ?
Forsøk å lage en tabell med de første 12 trekanttallene. Kontroller med tabellen nedenfor.
n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Trekanttall | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 | 78 |
Vi får for eksempel at .
Brøken er gjennomsnittet av tallene fra og med 1 til og med 7. Når vi multipliserer dette tallet med antall tall, som er 7, får vi summen av tallene fra og med 1 til og med 7.
Det betyr at formelen gir trekanttall nummer . Kontroller at denne formelen stemmer for de andre trekanttallene.
Et kvadrattall er et tall du får, når du opphøyer et helt tall i andre potens. Hva slags tall får du når du legger sammen to «nabo-trekanttall»?
_0.jpg?width=1024)
Blaise Pascal var en kjent fransk matematiker, fysiker, oppfinner og filosof som levde på 1600-tallet. En spesiell talltrekant har fått navnet etter Pascal selv om trekanten var kjent i mange hundre år før Pascal levde.
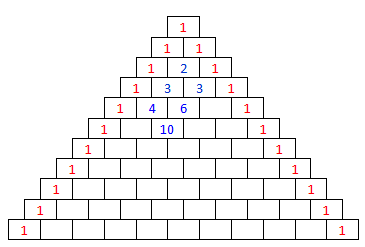
Lag en trekant av ruter som figuren ovenfor viser. Skriv inn tallet 1 i alle rutene langs kanten av trekanten. Vi har begynt å fylle inn tall i resten av rutene. Ser du hvordan vi har funnet disse tallene? Fortsett etter samme mønster, og fyll inn tall i alle rutene.
I trekanten ovenfor har vi valgt å lage 11 rader. Trekanten kan utvides etter samme mønster.
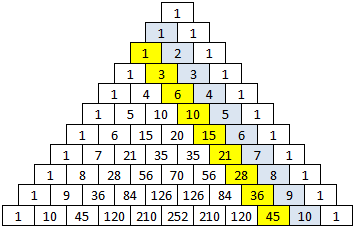
Se på tallene som er farget gule. Kjenner du igjen denne tallfølgen? Ganske riktig. Det er trekanttallene!
Ser du hvordan de framkommer etter følgende mønster?