Potensfunksjoner

Live arver kroner. Hun vil spare pengene.
Den lokale banken tilbyr en årlig rente på per år. Dette svarer til en vekstfaktor på . Live regner det som sannsynlig at hun vil få bruk for pengene om år. Hvor mye vil beløpet ha vokst til etter år?
Beløpet vil ha vokst til ca. kroner.
Live vet at det finnes alternativer til banksparing, og hun vil undersøke hva beløpet kan vokse til etter år, hvis renten er høyre enn .
Hun ser da at hun kan bruke funksjonen gitt ved
Her er det vekstfaktoren som er den variable, .
Live tegner grafen til for .
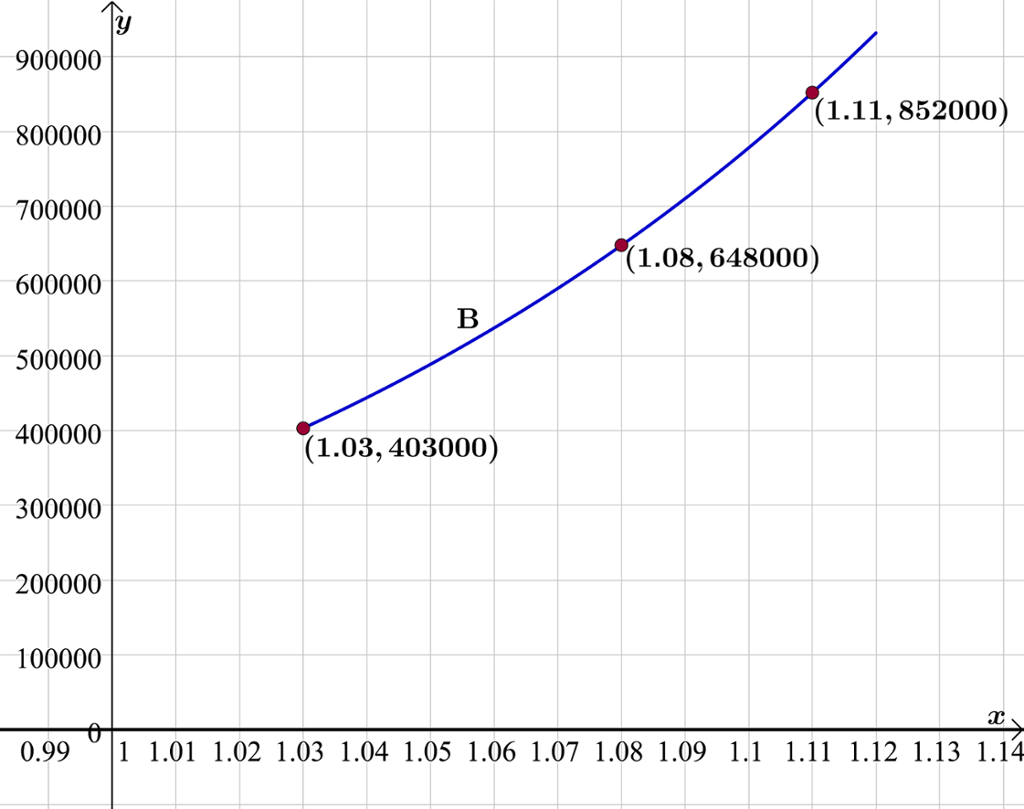
Av grafen kan hun se at ved en årlig rente på vil beløpet vokse til ca. kroner etter år. Hvis renten er på per år, vil beløpet vokse til ca. kroner og hvis hun kan få en rente på per år, altså at vekstfaktoren er , vil hun sitte med ca. etter år.
I funksjonsuttrykket er grunntallet i en potens hvor eksponenten er et konstant tall. En slik funksjon kalles for en potensfunksjon.
Potensfunksjoner
En funksjon gitt ved , hvor og er konstante tall, kalles en potensfunksjon.
Legg merke til at når er et ikkenegativt helt tall, er potensfunksjonen også en polynomfunksjon, som for eksempel , osv.
Når er et negativt helt tall, er potensfunksjonen en rasjonal funksjon, som for eksempel osv.
Når ikke er et helt tall, må vi forutsette at er positiv. Grunnen er at for eksempel betyr det samme som , og kvadratroten av et negativt tall er ikke et reelt tall.
Nedenfor har vi tegnet grafene til noen funksjoner gitt på formen . I tillegg kan du dra i glideren for å se hvordan funksjonen ser ut for andre verdier av .
Hvorfor går alle grafene gjennom punktet ?
Hvordan ser grafen ut når ?
Grafene endrer hovedform etter om , eller .
Legg merke til at grafen til en potensfunksjon gitt ved alltid går gjennom punktet fordi .

Når en pendel svinger, er svingetiden, det vil si den tiden det tar fra pendelen slippes til den kommer tilbake til utgangspunktet, avhengig av lengden på snoren som pendelkulen henger i.
Fra naturfag kjenner du kanskje formelen for svingetiden T sekunder, som funksjon av snorlengden meter?
Formelen gir at
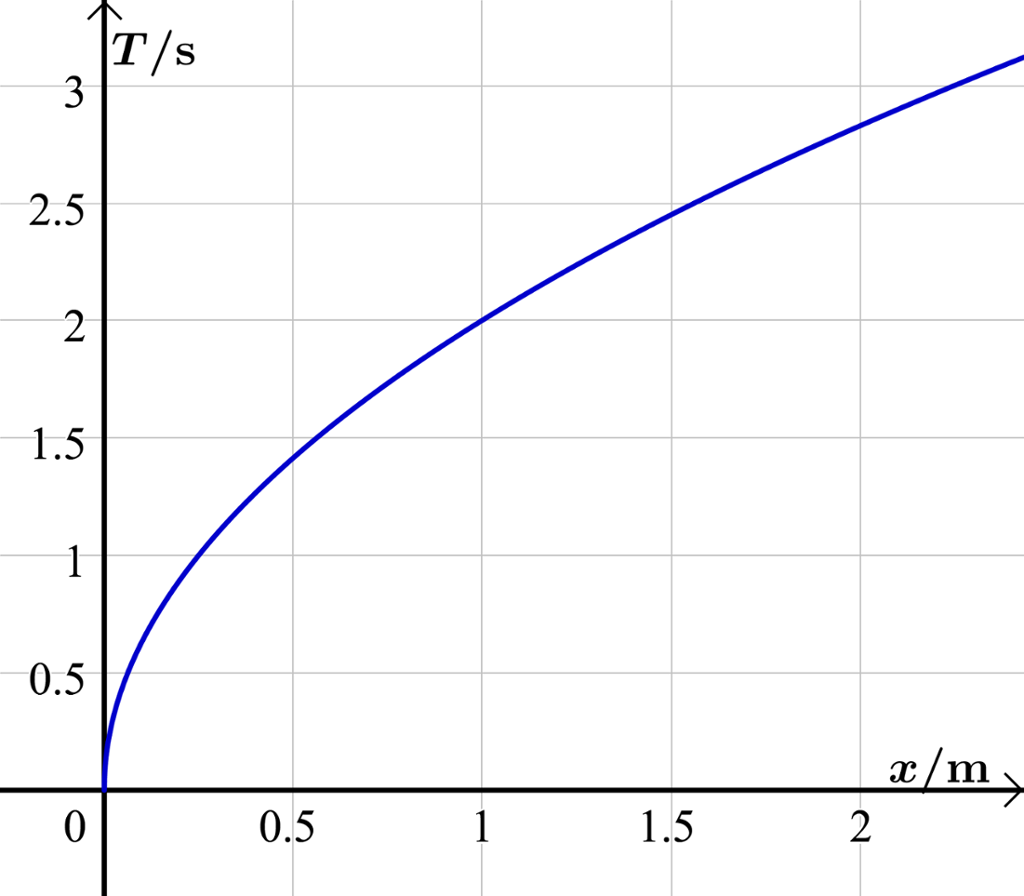
Her er og ( er tyngdens akselerasjon).
Når vi setter inn disse verdiene i formelen, får vi
Svingetiden til en pendel er altså en potensfunksjon av snorlengden.
Vi vet også at , slik at svingetiden kan uttrykkes som
Nå er svingetiden uttrykt som en funksjon.