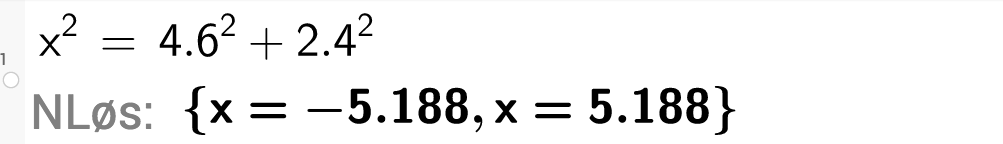Pytagorassetninga
Teikn ein trekant som er rettvinkla og der dei kortaste sidene er tre og fire einingar lange. Figuren viser ein slik trekant som er teikna i GeoGebra. Mål den lengste sida. Blir denne fem einingar lang?
Ta no alle dei tre sidelengdene og multipliser dei med seg sjølve. Du får då kvadratet av sidelengdene.
Kvadratet av sidelengda er
Kvadratet av sidelengda
Kvadratet av sidelengda
Samanlikn summen av kvadrata til dei to kortaste sidene med kvadratet til den lengste sida. Kva ser du?
Vi ser at
Det viser seg at denne samanhengen gjeld for alle trekantar som har ein vinkel på 90°.
For å kunne formulere denne samanhengen med ord gir vi namn på sidene i rettvinkla trekantar.
Den lengste sida i ein rettvinkla trekant kallar vi hypotenus. Dei to kortaste sidene kallar vi katetar.
Pytagorassetninga:
Legg merke til namnsetjinga. Vi bruker store bokstavar som namn på punkt eller hjørne i trekanten. Små bokstavar blir brukte som namn og måltal for sidelengdene. Det er vanleg at vi har den same bokstaven på motståande hjørne og sider.
Lag eit kvadrat med sidelengder
Del sidelengdene i to delar
Det grå arealet er eit kvadrat (kvifor?) med sidelengde
Flytt på trekantane inne i det store kvadratet som vist på neste figur. (I GeoGebra lagar du ei ny teikning. Bruk rutenett.)
Arealet av dei to store kvadrata er like store då sidelengdene er lik
Samla areal til dei fire rettvinkla trekantane er like store i begge figurane.
Det må bety at dei grå areala i dei to figurane er like store, altså at
Døme 1. Hypotenusen er ukjend
Vi ønskjer å finne ut kor lang sida
Sida
Døme 2. Kateten er ukjend
Vi ser no på den neste trekanten. Denne gongen vel vi å bruke CAS for å finne den ukjende sida ved hjelp av pytagorassetninga:
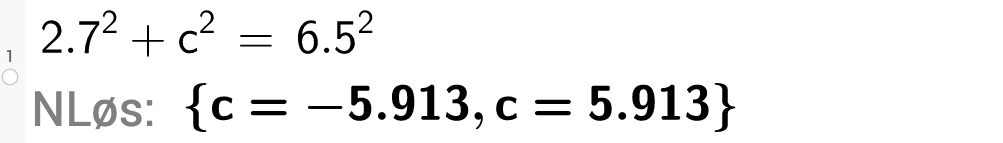
Sida
Døme 3. Eit praktisk døme
Ein stige skal plasserast 2,4 meter frå ein husvegg slik at han akkurat når opp til vindaugskarmen i eit vindauge i andre etasje. Vindaugskarmen er 4,6 meter over bakken.
Kor lang må stigen vere?
Her kan du sjå ein video som viser korleis ein kan bruke pytagorassetninga i praksis når ein skal lage rette vinklar.
Sjå videoen, og etterpå kan du kanskje bruke noko av det du lærte til å sjekke om hjørna i klasserommet ditt eller i stova heime er rette? Alt du treng, er ein tommestokk eller eit måleband!