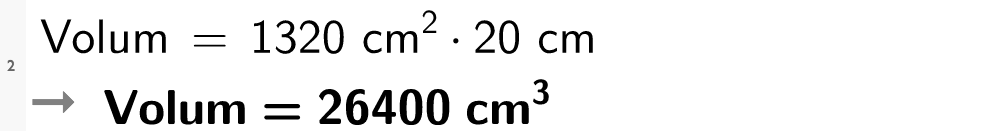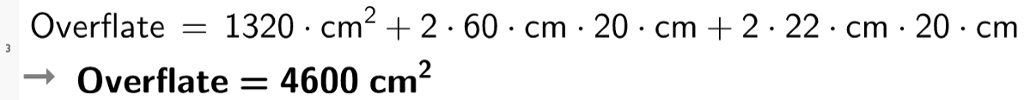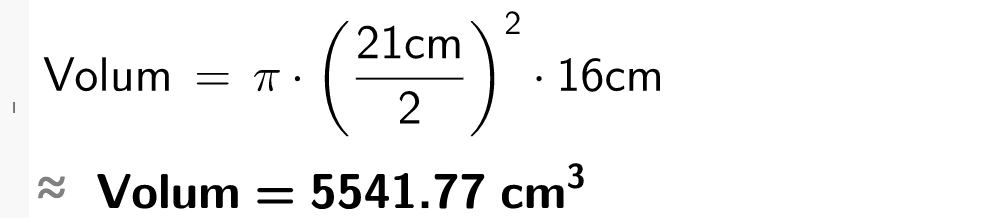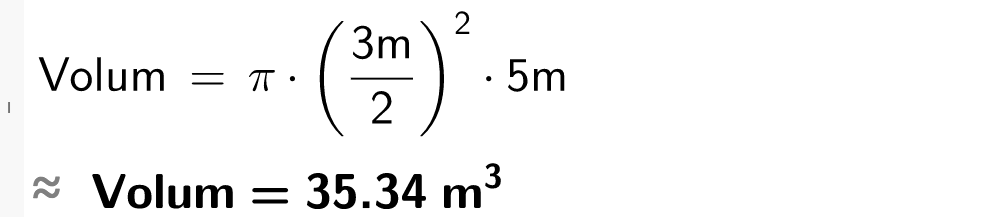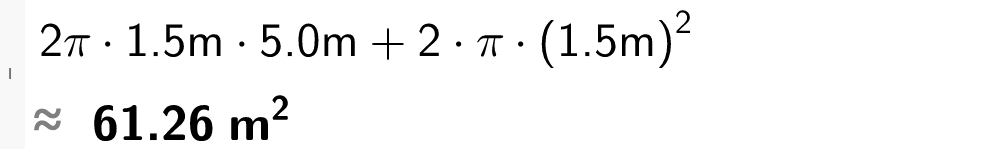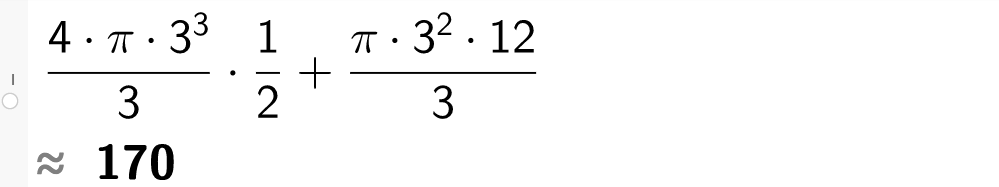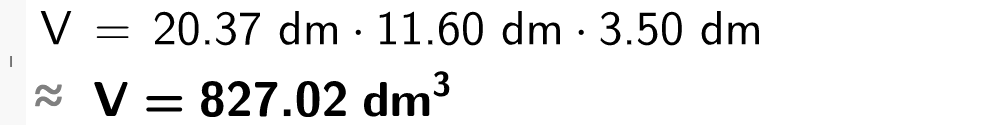Ein kartong med appelsinjus har desse måla: høgde 24,0 cm, breidde 6,6 cm og djupne 6,4 cm.
Løysing Kartongen rommar1 013 , 8 cm 3 = 1 , 0 dm 3 = 1 , 0 L
Det er planlagt å grave ut ein 2 km lang kanal. Kanalen skal vere 2,5 m djup, 5 m brei øvst og 2,5 m brei i botnen. Sidene skrånar jamt.
Kor mange kubikkmeter masse må gravast ut?
Løysing Talet på kubikkmeter som må gravast ut, er18 750 m 3
Ein kakeboks har form som ein sylinder. Kakeboksen har ein diameter på 21,0 cm og ei høgde på 16,0 cm. Kor mange liter rommar kakeboksen?
Løysing Kakeboksen rommar 5,54 liter.
Ein oljetank har form som ein sylinder. Oljetanken er 5,0 meter høg. Diameteren er 3,0 meter.
a) Kor mange liter olje rommar oljetanken?
Løysing Volumet av oljetanken er35 m 3 = 35 000 dm 3 = 35 000 liter
b) Rekn ut overflata av oljetanken.
Løysing Overflata O O = 2 π r · h + 2 · π r 2
Overflata av oljetanken er 61 m 2
Ei gryte har form som ein sylinder. Gryta har ein diameter på 260 mm og rommar 8 liter. Rekn ut høgda til gryta.
Løysing Høgda til gryta er 1 , 51 dm = 15 cm
Vi har gitt ein rett pyramide med kvadratisk grunnflate og høgde 6.
a) Rekn ut volumet av pyramiden.
Løysing V = G · h 3 = 4 · 4 · 6 3 = 32
b) Rekn ut høgda i trekanten som utgjer sideflata (dette er den stipla linja frå M til toppunktet).
Løysing Vi bruker pytagorassetninga:
h 2 = 2 2 + 6 2 = 40 h = 40 = 6 , 32 ≈ 6 , 3
c) Rekn ut overflatearealet til pyramiden.
Løysing Vi har fire trekantar som utgjer sidekantane, og eit kvadrat som utgjer grunnflata:
O = A □ + 4 · A △ = 4 · 4 + 4 · 4 · 6 , 3 2 = 16 + 4 · 2 · 6 , 3 = 16 + 50 , 4 = 66 , 4
Vi har gitt ei kjegle med radius 3,5 cm i grunnflata og som har sidekant lik 8,0 cm.
a) Rekn ut høgda i kjegla.
Løysing Vi bruker pytagorassetninga:
h = 8 , 0 2 - 3 , 5 2 = 51 , 75 = 7 , 19 ≈ 7 , 2
Høgda i kjegla er 7,2 cm.
b) Rekn ut volumet av kjegla.
Løysing Vi bruker formelen:
V = π r 2 · h 3 = π · 3 , 5 2 · 7 , 2 3 = 92 , 3 ≈ 92
Vi har at volumet er cirka 92 cm2 .
c) Rekn ut overflatearealet til kjegla.
Løysing Vi bruker formelen:
O = π r 2 + π r s = π 3 , 5 2 + π · 3 , 5 · 8 , 0 = 126
Overflatearealet til kjegla er 126 cm 2 ≈ 1 , 3 dm 2
Gitt ei kjegle med radius 12,0 cm og høgde 24,0 cm.
a) Finn volumet av kjegla.
Løysing Volumet av ei kjegle er gitt ved formelenV = π r 2 · h 3
Volumet av kjegla er 3 619 cm 3 ≈ 3 , 62 dm 3
b) Finn overflatearealet av kjegla.
Løysing Overflata av ei kjegle med botn er gitt ved formelenO = π r 2 + π r · s
Vi finn først sidekanten s
Overflata av kjegla er 1 464 cm 2 ≈ 14 , 6 dm 2
Ein kuleforma appelsin har ein diameter på 8,0 cm.
a) Finn overflata av appelsinen.
Løysing Overflata = 4 · π · r 2 = 4 · π · ( 4 , 0 cm ) 2 = 200 cm 2 = 2 , 0 dm 2
b) Forklar kva overflata er i praksis.
Løysing Overflata av appelsinen er arealet av skalet.
c) Finn volumet av appelsinen.
Løysing Volumet = 4 · π · r 3 3 = 4 · π · ( 4 , 0 cm ) 3 3 = 270 cm 3 = 0 , 27 dm 3
Skalet på appelsinen er 3 mm tjukt.
d) Finn volumet av den delen av appelsinen som går an å ete. (Sjå bort frå skalet, om du plar ete det ...)
Løysing Radiusen av sjølve appelsinkjøtet: 4 , 0 cm - 0 , 3 cm = 3 , 7 cm 4 · π · r 3 3 = 4 · π · ( 3 , 7 cm ) 3 3 = 210 cm 3 = 0 , 21 dm 3
e) Finn volumet av skalet.
Løysing Volumet av skalet er ytre volum minus indre, altså270 cm 3 - 210 cm 3 = 60 cm 3
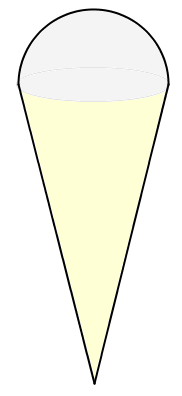
Ein kjeksis består av ein kjegleforma kjeks og ei halvkule med is øvst. Diameteren på kjeksen er 6,0 cm. Høgda på kjeksen er 12,0 cm.
a) Finn radiusen i kula.
Løysing Radiusen i kula er den same som radiusen på kjeksen, det vil seie 3,0 cm.
b) Finn volumet av kjeksisen.
Løysing Volumet av ei halvkule med is:4 · π · ( 3 , 0 cm ) 3 3 · 1 2
Volumet av ei kjegle med is:π · ( 3 , 0 cm ) 2 · 12 , 0 cm 3
Samla mengde is blir170 cm 3 = 0 , 17 L = 1 , 7 dL
Ein tilhengjar har dei følgjande måla:
a) Kor mange liter rommar tilhengjaren?
Løysing Vi løyser oppgåva i GeoGebra:
Tilhengjaren rommar 827 liter.
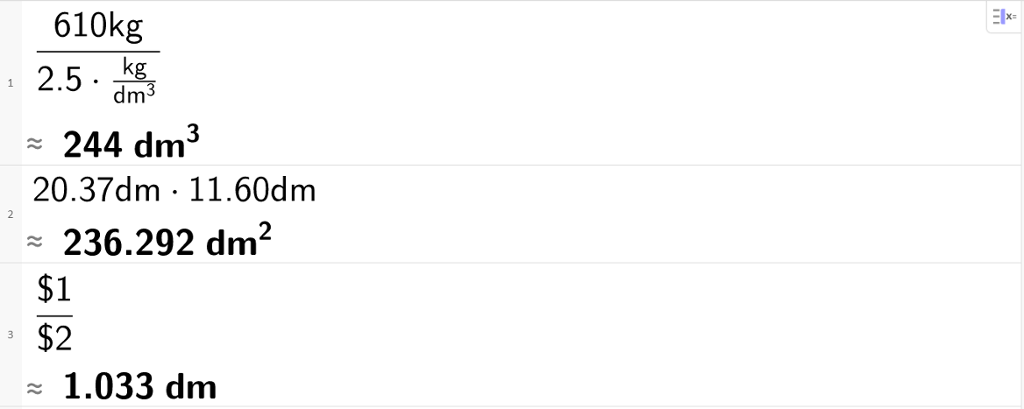
b) Den største nyttelasta tilhengjaren kan ha, er 610 kg. Kor tjukt lag med grus kan du fylle oppi tilhengjaren når 1 liter grus veg 2,5 kg?
Løysing Her kan det vere greitt å setje opp ei likning. Vi kan rekne ut massen i kg ved å multiplisere talet på liter grus med talet på kg grus per liter. Talet på liter grus får vi ved å multiplisere lengda med breidda og vidare med den ukjende høgda, som vi her kallar h
Vi får
20 , 37 dm · 11 , 60 dm · h · 2 , 5 kg dm 3 = 610 kg
Her har vi teke med einingane for å kontrollere at vi ikkje har andre typar enn dm og kg. Når vi løyser dette i GeoGebra, kan vi skrive inn einingane og få talsvaret med riktig eining i tillegg. Då må vi i tilfelle bruke kommandoen Løys(likning, variabel) saman med knappen for numerisk utrekning:≈
Det kan fyllast eit gruslag med ei tjukne på 1 , 03 dm = 10 , 3 cm
Alternativ løysing Vi finn først ut kor mange liter grus vi får av 610 kg. Deretter reknar vi ut arealet av grunnflata i tilhengjaren. Til slutt tek vi volumet av grus og deler på grunnflata for å finne høgda. Vi tek heile tida med einingane i CAS-utrekninga som kontroll.
Ei tresøyle har form som ein sylinder med diameter 30 cm og høgde 4,20 m. Søyla skal få to strøk måling. Ein liter måling dekkjer 6 m2 . Kor mykje måling vil gå med?
Løysing Vi reknar ikkje topp og botn i dette tilfellet.
Det vil gå med 1,3 liter måling.
Ei kjegle har radiusen 2,4 dm og ein sidekant på 6,4 dm.
a) Finn høgda i kjegla.
Løysing Vi bruker pytagorassetninga og finn høgda:
( sidekant ) 2 = ( radiusen ) 2 + ( høgda ) 2 s 2 = r 2 + h 2
Høgda er 5,9 dm.
b) Finn volumet av kjegla.
Løysing Volumet er 36 dm 3