Fagartikkel

Definisjon av vektor

Vektorar er storleikar som i tillegg til eit måltal (ei lengde) òg har ei retning.

Kva er ein vektor?

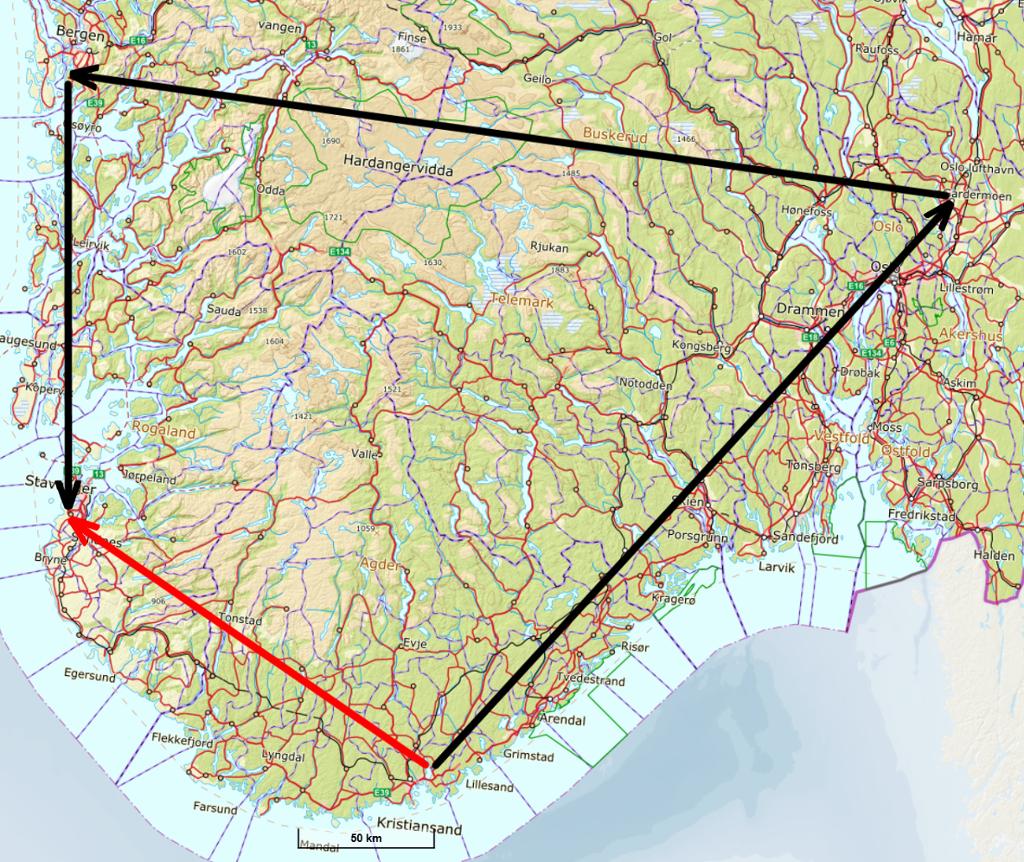
Kart over den sørleglaste delen av Noreg. Fire piler på kartet dannar ein firkant. Ei svart pil går frå Oslo Gardermoen til Bergen Flesland, ei svart pil går frå Bergen Flesland til Stavanger Sola, ei svart pil går frå Kristiansand Kjevik, og ei raud pil går frå Kristiansand Kjevik til Stavanger Sola. Illustrasjon. — Kjelde: Statens kartverk. Bilete: Statens kartverk / CC BY-NC-SA 4.0

Tenk deg ei flyreise som startar i Kristiansand, går via Oslo og Bergen og endar i Stavanger. Reisa kan illustrerast med piler som vist på kartet.

Pilene illustrerer dei aktuelle forflyttingane. Lengdene på pilene fortel om lengdene på flyreisene, og retningane på pilene fortel om retningane på reisene.

Dersom formålet med flyreisa var å flytte seg frå Kristiansand til Stavanger, kunne alle flyreisene vore erstatta av ei einaste flyreise, nemleg direkte frå Kristiansand til Stavanger. Den raude pila viser denne reisa, som vi kan seie er "sluttresultatet" eller "summen" av alle reisene.

Forflytting er eit døme på ein storleik der vi må kjenne til både lengda og retninga for å beskrive storleiken fullstendig. Frå naturfag (fysikk) kjenner du omgrepa kraft, fart og akselerasjon. Dette er òg storleikar med retning. Det har vist seg svært formålstenleg å teikne desse storleikane som piler. Slike storleikar som har både lengde og retning, kallar vi vektorar, og storleikane kallar vi vektorstorleikar eller berre vektorar.

Ein storleik som ikkje har retning, kallar vi ein skalar. Eit pengebeløp er eit døme på ein skalar.

Eit døme på korleis vi set namn på vektorar. Fire piler, altså vektorar, har fått namna a, b, AB og HG. Ei lita pil som går rett bortover frå venstre til høgre står over alle namna. Illustrasjon. — Bilete / CC BY-SA 4.0

Når vi skal gi vektorar namn, bruker vi bokstavar med ei pil over. Det er vanleg å bruke små bokstavar, som figuren viser.

Når ein vektor går frå eit punkt til eit anna, bruker vi store bokstavar. Vektoren mellom to punkt $A$ og $B$ får namnet $\vec{A B}$ . Vi seier at denne vektoren har utgangspunkt i $A$ og endepunkt i $B$ . Kva er forskjellen på $\vec{A B}$ og $\vec{B A}$ ?

Ein vektor har altså både lengde og retning. La $\vec{s}$ vere forflytting 3 kilometer vestover. Vi seier at lengda av vektoren er 3 kilometer, og at retninga er vestover. Når vi skal beskrive ein vektor, er det viktig å skilje klart mellom desse to eigenskapane.

Lengda av ein vektor

Frå før veit du kanskje kva vi meiner med absoluttverdien til eit tal. Vi kan sjå på det som lengda på talet eller avstanden frå 0 til talet. Vi noterer det slik:

$|t|$ er absoluttverdien til talet $t$ .

$\begin{array}{rcl} |t| & = & t viss t \geq 0 . \\ |t| & = & - t viss t < 0 . \end{array}$

Absoluttverditeikn blir òg brukt for å nemne lengda av ein vektor. Vi skriv at:

$|\vec{s}| = 3 km$

Lengda av ein vektor er altså ein skalar, mens vektoren sjølv er bestemd ved både ei lengde og ei retning.

Dersom du kan parallellforskyve ein vektor slik at han dekkjer ein annan vektor, er dei to vektorane like.

Dette betyr til dømes at dersom vi flyttar den raude vektoren som går frå Kristiansand til Stavanger slik at han startar i Oslo og går i nord-vestleg retning til områda rundt Hemsedal, vil vi ha den same vektoren sjølv om han er teikna ein annan stad i kartet.

Ein storleik som har ei bestemd lengde og ei bestemd retning, kallar vi ein vektor.

Ein skalar er ein storleik utan retning.

Døme på vektorar er forflytting, fart og kraft.

Døme på skalarar er temperatur, areal og volum.

Vi kan teikne ein vektor som ei pil.

Ein vektor er ikkje "stadbunden". Om vi flyttar ein vektor slik at han beheld både lengde og retning, så er det framleis den same vektoren.

Med $|\vec{s}|$ meiner vi lengda av $\vec{s}$ .

Med $- \vec{s}$ meiner vi ein vektor som er parallell med og har same lengde som $\vec{s}$ , men er motsett retta.

Nullvektoren er ein vektor med lengde null. Han har inga retning og blir skriven som $\vec{0}$ .

Video om vektorar

Video: Tom Jarle Christiansen / CC BY-SA 4.0