Pris og etterspørsel
Inntektsfunksjonen
En bedrift kan ikke bare bestemme prisen på en vare, forutsette at alt blir solgt, og ut ifra dette beregne den produksjonen som gir størst overskudd. Kanskje prisen er satt så høyt at ikke alle varene blir solgt?
Vi ser på et eksempel fra siden Kostnads-, inntekts- og overskuddsfunksjon. Klasse 3STB har kommet fram til at inntektsfunksjonen ved salg av treningsapparatet Multiform er gitt ved
Inntekten ved salg er alltid lik prisen per enhet multiplisert med antall solgte enheter. Hvis vi forutsetter at alle produserte enheter blir solgt, er
Prisfunksjonen
I dette eksempelet kan vi komme fram til en funksjon for prisen
Det betyr at vi kan se på faktoren
Prisfunksjonen er lineær med negativt stigningstall. Vi ønsker å finne verdimengden
Hva blir verdimengden ut ifra dette?
Aktivitet
Siden prisen er en funksjon av antall enheter, er antall enheter avhengig av prisen. Endre på likningen
Tenk over
Hva betyr dette resultatet i praksis?
Dette kalles for etterspørselsfunksjonen, og denne funksjonen viser hvor mange enheter vi kan få solgt ved en bestemt pris. Produksjonen kan da tilpasses salget.
Når etterspørselen som funksjon av prisen er
Finn inntektsfunksjonen
Inntektsfunksjoner kan generelt skrives som
Finn kostnadsfunksjonen
Finn kostnadsfunksjonen
Kostnads- og inntektsfunksjonen med CAS
Bruk CAS til å finne
Vi viser resten av eksempelet med bruk av CAS. Overskuddsfunksjonen finner vi som før ved å se på forskjellen mellom inntekten og kostnadene. Så finner vi det største overskuddet som toppunktet til funksjonen.
Overskuddsfunksjonen
Bruk CAS, finn overskuddsfunksjonen
Siden overskuddsfunksjonen er en andregradsfunksjon med negativ koeffisient foran andregradsleddet, vet vi at funksjonen har et toppunkt. Det største overskuddet får elevene derfor når prisen er 670 kroner.
Til slutt regner vi ut hvor stort overskuddet blir med denne prisen, og vi må finne ut hvor mange enheter (trimapparater) vi skal produsere.
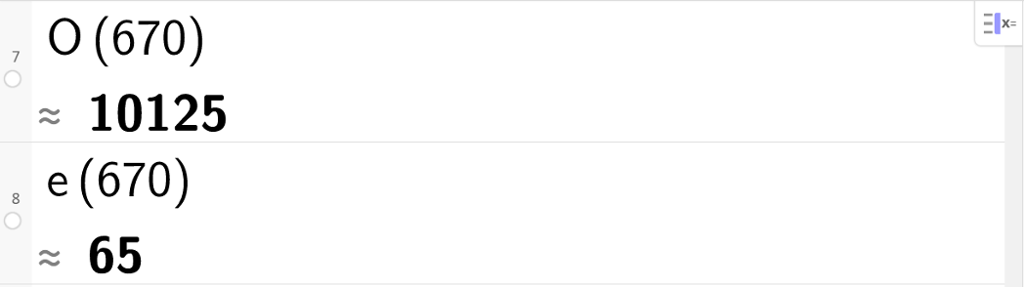
Det maksimale overskuddet er på 10 125 kroner per uke. Etterspørselen ved denne prisen er 65 enheter.
Dette er det samme antall enheter som vi har funnet på siden Kostnads-, inntekts- og overskuddsfunksjon. Det skyldes at vi tok utgangspunkt i den opprinnelige inntektsfunksjonen
Grafisk løsning
Vi får det samme resultatet grafisk.
Vi kan i tillegg finne hvilke priser vi må holde oss innenfor hvis vi skal gå med overskudd. Da kan vi for eksempel finne nullpunktene til overskuddsfunksjonen
Tenk over
I utgangspunktet hadde elevene tenkt å selge treningsapparatet til 800 kroner. Hva betyr det at den prisen som gir størst overskudd, er 670 kroner?

