Fagstoff

Grensekostnad og grenseinntekt

Når en bedrift skal bestemme hvor mye de skal produsere, er begreper som grensekostnad og grenseinntekt viktige.

Grensekostnad

Grensekostnad, definisjon

Grensekostnaden er kostnaden ved å produsere én ekstra enhet av en vare ved en gitt produksjonsmengde.

Kostnadsfunksjon, grensekostnad og momentan vekstfart

Vi går ut ifra at vi har en kostnadsfunksjon $K (x)$ å ta utgangspunkt i. Grensekostnaden når produksjonen for eksempel ligger på 1 000 enheter, det vil si endringen i kostnadene ved å øke produksjonen fra 1 000 til 1 001, kan vi regne ut med $K (1 001) - K (1 000)$ . Men vi har også en annen måte å gjøre dette på.

Vi kan omformulere definisjonen av grensekostnaden til å være hvor mye kostnaden endrer seg per enhet ved en gitt produksjonsmengde. Dette er det samme som den momentane vekstfarten til kostnadsfunksjonen i dette punktet.

Eksempel: elevbedrift

Vi skal prøve dette på eksempelet med elevbedriften som skal produsere treningsapparatet Multiform, se siden Kostnads-, inntekts- og overskuddsfunksjon.

Elevene i elevbedriften har kommet fram til kostnadsfunksjonen

$K (x) = 3 x^{2} + 150 x + 11 000, D_{K} = [0, 150]$

Vi ønsker å finne grensekostnaden når produksjonen er på 20 enheter og på 100 enheter. På figuren nedenfor har vi tegnet kostnadsfunksjonen i det aktuelle området sammen med de to punktene på grafen der $x = 20$ og $x = 100$ . Vi har også tegnet tangentene i disse punktene.

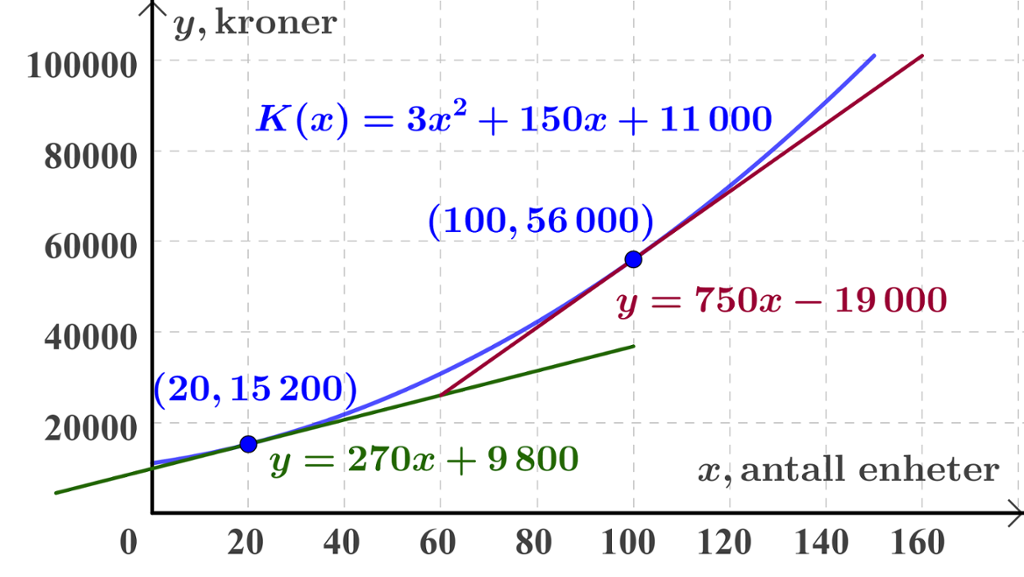
Illustrasjon av koordinatsystem. Grafen til funksjonen K av x er lik 3 x i andre pluss 150 x pluss 11000 er tegnet for x-verdier mellom 0 og 150. I tillegg er tangentene i punktene på grafen der x er lik 20 og x er lik 100, tegnet inn. Den første tangenten har stigningstall lik 20, den andre tangenten har stigningstall lik 100.

Vi kan nå finne fra stigningstallet til tangenten at den momentane vekstfarten til kostnadsfunksjonen når $x = 20$ , er 270 kroner per enhet. Da sier vi at grensekostnaden ved 20 produserte enheter er 270.

Hva betyr egentlig dette?

Betydning

Det betyr at det koster elevbedriften 270 kroner å øke produksjonen fra 20 til 21 enheter.

Tenk over hvordan vi kan finne grensekostnaden ved 20 produserte enheter ved regning. I boksen nedenfor ser du hvordan vi har gjort det.

Grensekostnaden ved regning

Siden grensekostnaden er det samme som den momentane vekstfarten til kostnadsfunksjonen, kan vi finne grensekostnaden ved å regne ut den deriverte i punktet, $K^{'} (20)$ . Ofte kaller vi rett og slett den deriverte funksjonen $K^{'} (x)$ bare for "grensekostnaden".

Vis ved regning at grensekostnaden når $x = 20$ , er 270.

Ved regning

Vi deriverer kostnadsfunksjonen:

$K (x) = 3 x^{2} + 150 x + 11 000$

$K^{'} (x) = 3 \cdot 2 x + 150 = 6 x + 150$

$K^{'} (20) = 6 \cdot 20 + 150 = 120 + 150 = 270$

Bruk figuren og finn grensekostnaden i eksempelet når elevbedriften produserer 100 enheter. Regn deretter ut det samme ved å bruke $K^{'} (x)$ .

Grensekostnad ved 100 produserte enheter

Vi leser av stigningstallet til den andre tangenten i figuren over at den momentane vekstfarten er 750 når $x = 100$ .

Vi regner så ut det samme ved hjelp av $K^{'} (x)$ :

$K^{'} (100) = 6 \cdot 100 + 150 = 600 + 150 = 750$

Grensekostnaden ved 100 produserte enheter er derfor 750 kroner. Det betyr at når produksjonen ligger på 100 enheter, koster det elevbedriften 750 kroner å øke produksjonen med én enhet.

Tenk over hvilke grunner det kan være til at grensekostnaden når $x = 100$ , er mye større enn grensekostnaden når $x = 20$ . Sagt med andre ord: Hvorfor er det mye dyrere å produsere én enhet ekstra når produksjonen ligger på 100 enheter, enn på 20 enheter?

Forklaring

Det enkle, matematiske svaret er: fordi grafen til kostnadsfunksjonen er brattere når $x = 100$ , enn når $x = 20$ . En mulig forklaring på hvorfor det er slik, er at når det produseres mye fra før, må elevene kanskje bruke overtid, sette flere folk i arbeid, kjøpe inn mer produksjonsutstyr eller liknende, som gjør at kostnadene øker mye. Når bedriften produserer lite, slipper man å gjøre slike grep. Se også teorisiden om kostnads-, inntekts- og overskuddfunksjoner der dette er diskutert.

Grensekostnad, definisjon og oppsummering

Grensekostnaden er endringen i kostnadene ved å produsere én ekstra enhet av en vare ved en gitt produksjonsmengde.

Vi kan finne grensekostnaden i et punkt ved å finne den momentane vekstfarten til kostnadsfunksjonen i punktet.

Ofte kaller vi bare den deriverte av kostnadsfunksjonen, $K^{'} (x)$ , for grensekostnaden.

Grenseinntekt

Grenseinntekt blir definert tilsvarende som grensekostnad.

Grenseinntekt, definisjon og oppsummering

Grenseinntekten er endringen i inntektene ved å selge én ekstra enhet av en vare ved en gitt mengde solgte enheter.

Vi kan finne grenseinntekten i et punkt ved å finne den momentane vekstfarten til inntektsfunksjonen i punktet.

Ofte kaller vi bare den deriverte av inntektsfunksjonen, $I^{'} (x)$ , for grenseinntekten.

Grenseinntekt for elevbedriften

Elevbedriften som selger treningsapparatet Multiform, har kommet fram til at inntektsfunksjonen $I$ er

$I (x) = 800 x - 2 x^{2}$

Vi ønsker å finne grenseinntekten ved 20 solgte enheter. Det kan vi gjøre ved å derivere inntektsfunksjonen og regne ut $I^{'} (20)$ .

$I^{'} (x) = 800 - 2 \cdot 2 x = 800 - 4 x$

$I^{'} (20) = 800 - 4 \cdot 20 = 800 - 80 = 720$

Grenseinntekten ved 20 solgte enheter er 720 kroner. Det betyr at elevene forventer at inntekten øker med 720 kroner dersom de selger ett treningsapparat ekstra når produksjonen ligger på 20 enheter i uka.

Prøv selv: Finn grenseinntekten ved 100 solgte enheter.

Grenseinntekten ved 100 solgte enheter

Vi regner ut

$I^{'} (100) = 800 - 4 \cdot 100 = 800 - 400 = 400$

Grenseinntekten ved 100 solgte enheter er 400 kroner. Det betyr at elevene forventer at inntekten øker med 400 kroner dersom de selger ett treningsapparat ekstra når produksjonen er på 100 enheter i uka.

Sammenlikn de to tallene for grenseinntekten.

Sammenlikning

I utgangspunktet skulle man tro at inntekten alltid øker med 800 kroner når de selger ett apparat ekstra, siden prisen på treningsapparatet er 800 kroner. Av diskusjonen rundt fastsettelsen av inntektsfunksjonen på siden om kostnads-, inntekts- og overskuddfunksjoner går det fram at når produksjonsmengden øker, det vil si at tilbudet blir større, vil etterspørselen generelt bli mindre. Det blir også sagt at et stort salg vil inkludere salg av større partier til sportsbutikker, og at man ikke kan regne med å få like høy pris da. Så jo flere apparater som blir solgt, jo lavere blir prisen, og jo lavere blir grenseinntekten.

Mer om grensekostnad og grenseinntekt

Vi fikk fra avsnittene over at

$K^{'} (20) = 270, I^{'} (20) = 720$
$K^{'} (100) = 750, I^{'} (100) = 400$

Vi får at når produksjonen ligger på 20 enheter per uke, koster det 270 kroner å produsere én enhet ekstra. Men samtidig øker inntekten med 720 kroner. Det betyr at overskuddet øker, så det vil lønne seg å øke produksjonen – hvis man antar at de får solgt alle 21 apparatene.

Hva skjer med overskuddet dersom produksjon (og salg) ligger på 100 enheter og elevbedriften ønsker å øke produksjonen?

Når produksjon og salg ligger på 100 enheter

Vi får at når produksjonen ligger på 100 enheter per uke, koster det 750 kroner å produsere én enhet ekstra. Samtidig øker inntekten med bare 400 kroner. Overskuddet vil derfor minke, så elevbedriften vil tape på å øke produksjonen selv om de får solgt alle de 101 apparatene.

Hva kan vi konkludere ut ifra dette?

Konklusjon

Så lenge grenseinntekten er større enn grensekostnaden, vil det lønne seg å øke produksjonen. Slik vil det være til vi kommer til det punktet der grenseinntekten og grensekostnaden er like.

Den deriverte av overskuddsfunksjonen

Vi kan vise at konklusjonen vi kom fram til over, gjelder generelt.

Vi har fra teorisiden om kostnads-, inntekts- og overskuddsfunksjoner at det største mulige overskuddet en bedrift kan ha, er der overskuddsfunksjonen har sin største verdi. Som regel finner vi denne verdien i et toppunkt der den deriverte er lik 0. Vi kan se for oss situasjoner der det største overskuddet finnes enten i et endepunkt eller i et knekkpunkt, men disse situasjonene er spesialtilfeller.

Vi har generelt at

$O (x) = I (x) - K (x)$

Vi prøver å derivere det generelle uttrykket for overskuddsfunksjonen:

$O^{'} (x) = I^{'} (x) - K^{'} (x)$

Hva får vi dersom vi setter den deriverte, $O^{'} (x)$ , lik 0, slik vi vanligvis gjør når vi skal finne de stasjonære punktene til en funksjon?

Resultat

$\begin{array}{rcl} O^{'} (x) & = & 0 \\ I^{'} (x) - K^{'} (x) & = & 0 \\ I^{'} (x) & = & K^{'} (x) \end{array}$

Vilkår for størst mulig overskudd

Det største mulige overskuddet er der hvor den deriverte av inntektsfunksjonen er lik den deriverte av kostnadsfunksjonen.

$I^{'} (x) = K^{'} (x)$

Vi kan også si at det største mulige overskuddet er der grensekostnaden er lik grenseinntekten.

I tillegg må vi sjekke om maksimalverdien til overskuddsfunksjonen kan ligge i noen av endepunktene til funksjonen eller i et knekkpunkt der den deriverte ikke eksisterer.

CC BY-SASkrevet av Bjarne Skurdal, Olav Kristensen og Stein Aanensen.

Sist faglig oppdatert 20.01.2023