Kostnads-, inntekts- og overskuddsfunksjon

Inntektene og kostnadene til en bedrift vil variere med hvor mye som produseres. Det vil som regel være slik at jo mer som produseres, jo høyere blir både inntekter og kostnader. Overskuddet til en bedrift øker ikke nødvendigvis selv om bedriften får økt salget. Det hjelper ikke at bedriften tjener 5 000 kroner mer ved et økt salg av noen varer dersom det koster 10 000 kroner å produsere de ekstra varene. Bedriften må derfor ha god oversikt over hvordan kostnadene varierer med hvor mye de produserer.
Overskuddet en bedrift får, kan vi regne ut ved å trekke kostnaden ved produksjonen fra inntekten ved salget. Dersom det koster bedriften 20 000 kroner å produsere en viss varemengde og inntekten fra salget er 30 000 kroner, vil overskuddet bli
Vi kan derfor lage oss følgende formel:
Overskudd
Husk at inntekt ikke er penger de kan stikke rett i lomma! Inntektene må brukes til å betale kostnadene. Så er håpet at det er igjen noe etter at kostnadene er betalt slik at de går med overskudd.
Prøv selv
Hva er inntekten av et salg dersom overskuddet er 45 000 kroner og kostnadene ved produksjonen er 25 000 kroner?
Dersom vi kan lage funksjoner for inntektene og kostnadene, får vi en god oversikt over hvordan overskuddet kan variere med antall. Dersom
Kostnadsfunksjon:
K x Inntektsfunksjon:
I x Overskuddsfunksjon:
O x
Sett opp et generelt uttrykk for overskuddsfunksjonen
Klasse 3STB ønsker å starte en elevbedrift for å produsere et treningsapparat de kaller Multiform. Vi skal bruke dette som eksempel.
Kostnadsfunksjon
Klassen lar
For hvert treningsapparat som produseres, går det med en bestemt mengde komponenter, som kjøpes inn til enhetspriser. Det kreves også et visst antall arbeidstimer for montering av hver enhet. Klassen beregner disse utgiftene til 150 kroner per enhet, og i en kostnadsfunksjon gir dette førstegradsleddet 150
Klassen regner med at det enkelte uker blir nødvendig med ekstra høy produksjon. Da kan det bli nødvendig med overtid, og kanskje de må sette flere elever i arbeid med produksjonen. Slike ekstrautgifter vil være lave ved liten produksjon og store ved høy produksjon. Læreren til elevene foreslår derfor at kostnadsfunksjonen også skal inneholde leddet
Alle er enige om at de med normal innsats vil klare å produsere og selge 130 treningsapparater per uke, men også at de med noen grep kan klare å produsere og selge 150. Det betyr at definisjonsområdet til kostnadsfunksjonen vil være fra og med 0 til og med 150.
Hvis klassen tar utgangspunkt i dette, vil kostnadene per uke ved produksjon av
Elevene er enige om at produksjonskostnadene foreløpig er meget usikre. De er derfor innstilt på å justere modellen når de ser de virkelige utgiftene.
Enhetskostnad
Hvis vi ønsker å regne ut kostnaden per enhet, må vi dele de totale kostnadene på antall produserte enheter. Dette gir følgende funksjon for enhetskostnaden i eksempelet over:
Inntektsfunksjon
Klassen vurderer hvilken pris de skal sette på Multiform. Elevene er enige om at 800 kroner er en passe pris på produktet.
Hva blir inntektsfunksjonen
Trym er litt skeptisk og sier: "En slik funksjon passer dårlig overens med at når det blir god tilgang på en vare, vil prisen synke. En annen ting er at for å oppnå et stort salg er vi avhengige av å selge større partier til sportsbutikker, som selger videre for oss. Da må vi nok regne med en lavere pris enn om vi selger alt selv."
Klassen er helt enig med Trym, og læreren til elevene foreslår at de må ha et ledd av typen
Elevene tegner grafen til
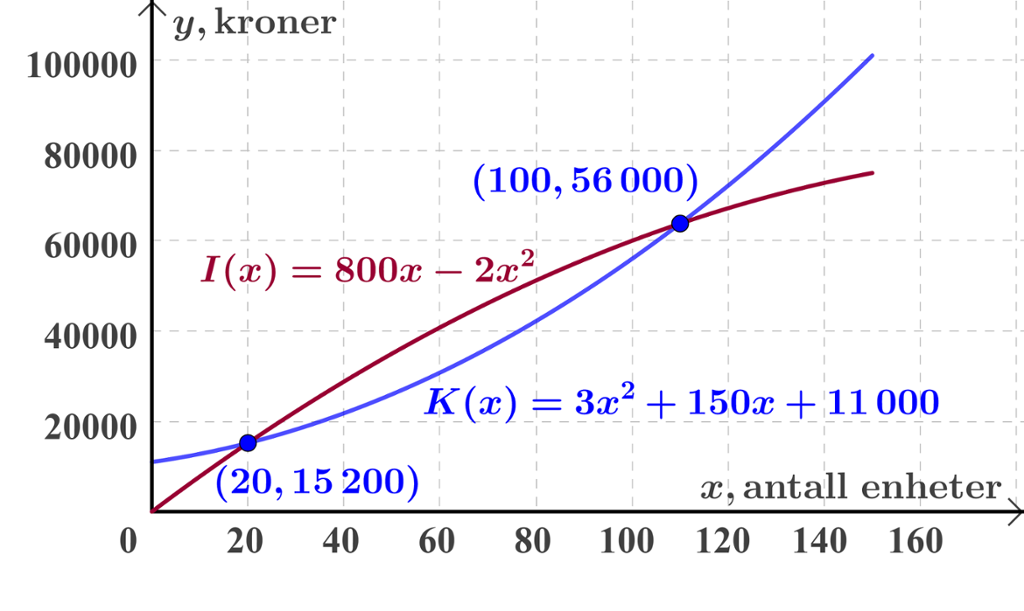
Hjelp elevene i 3STB med å tolke den grafiske framstillingen. Skriv ned noen punkter om hva du kan lese ut av diagrammet.
Overskuddsfunksjon
For å finne hvor mange treningsapparater elevbedriften skal produsere for å oppnå størst overskudd, kan de finne overskuddsfunksjonen.
Hjelp elevene å finne overskuddsfunksjonen.
Klassen tegner grafen til overskuddsfunksjonen O(x) = I - K i algebrafeltet til GeoGebra siden de har lagt inn inntekts- og kostnadsfunksjonen fra før.
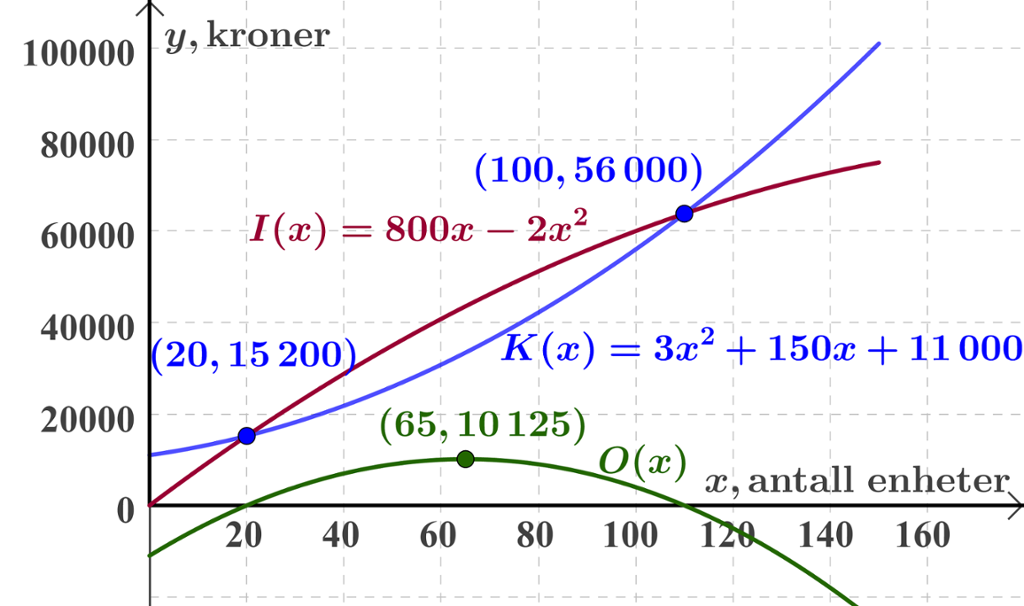
Det største overskuddet må være der grafen til
Vi kan også finne det største overskuddet med CAS.
Trenger vi å ha med utregningen i linje 5?