Rasjonale tall, reelle tall og tallintervall
Du kjenner også til regneoperasjonen divisjon. Vi kan dividere 8 med 4 og få 2, som er et helt tall. Men hvis vi for eksempel dividerer 1 med 2, blir resultatet ikke et helt tall. Vi får brøken . For å kunne dividere hele tall, må vi på ny utvide tallmengden vår. Vi må inkludere alle tall som består av brøker med hele tall i teller og nevner.
Husk at i en brøk er telleren "på toppen" og nevneren "nede".
Tall som kan skrives som brøker med hele tall i teller og nevner, kalles rasjonale tall. Disse symboliseres med .
Rasjonale tall blir ofte enklere å behandle hvis vi skriver dem som desimaltall. Prinsippet er at vi gjør brøkene om til brøker med 10, 100, 1000, osv. som nevnere.
Tenk deg at du deler en kake i ti like store deler. Fem av disse delene utgjør da halvparten av kaken.
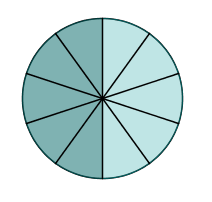
Det betyr at .
Et desimaltall har et desimalskilletegn. I Norge bruker vi komma som desimalskilletegn, mens de fleste andre land, og de fleste digitale verktøy bruker punktum. Første siffer etter desimalskilletegnet angir hvor mange tideler vi har, det neste hvor mange hundredeler vi har osv. Sifrene foran desimalskilletegnet angir heltall.
Det betyr at brøken kan skrives som .
Alle brøker kan på tilsvarende måte gjøres om til desimaltall.
For eksempel er
Vi kan nå anvende regneoperasjonene addisjon, subtraksjon, multiplikasjon og divisjon på rasjonale tall og få et rasjonalt tall som resultat.
Har vi så fått med oss alle tallene? Svaret er nei.
Bruk for eksempel GeoGebra. Lag sirkler i ulik størrelse og finn forholdet mellom omkrets og diameter. Forklar hvorfor vi kan finne omkretsen av en sirkel ved hjelp av formelen når vi kjenner radius.

Forholdet mellom omkretsen og diameteren i en sirkel er lik det tallet som vi kaller (pi). Du har lært at er en god tilnærmet verdi for , men faktisk er det ikke mulig å skrive som et rasjonalt tall. I 2009 ble tallet beregnet med en nøyaktighet av 2 699 999 990 000 desimaler. Det vil si nesten billioner desimaler. Tallet er et reelt tall, men er altså ikke rasjonalt. Vi sier at det er irrasjonalt.
Et annet irrasjonalt tall er det tallet som multiplisert med seg selv gir tallet 2. Vi skriver bare . Det finnes ingen brøker som multiplisert med seg selv gir tallet 2.
Vi må altså utvide tallmengden vår igjen for å få med slike tall som og . Den tallmengden vi nå har fått, kalles for de reelle tall, og den symboliseres med bokstaven .
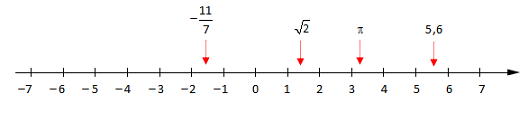
Vi kan tenke oss alle reelle tall som punkter på en uendelig lang rett linje, tallinjen. Punktene ligger veldig tett. Mellom to reelle tall er det uendelig mange reelle tall. Spørsmålet er så om vi nå har fått med oss alle tall? Svaret er igjen nei.
Det finnes for eksempel ikke noe reelt tall som multiplisert med seg selv gir tallet . er et imaginært tall. Vi skal ikke regne med imaginære tall i 1T-kurset, men bruk gjerne Internett og finn ut mer om imaginære og komplekse tall! (Komplekse tall er tall som inneholder en reell del og en imaginær del.)
Når vi skal referere til bestemte tall på tallinjen, bruker vi klammeparenteser . Mengden av de naturlige tallene 1, 2 og 5 skrives som .
Mengden av alle reelle tall avgrenset av to verdier kalles et tallintervall. Eksempler på tallintervaller er
og
Det første intervallet inkluderer tallene 1 og 3 i tillegg til alle reelle tall mellom disse to tallene. Dette er et lukket intervall.
I det andre intervallet er 1 og 3 ikke med, men ellers er alle tallene som er med i det første intervallet også med her. Dette er et åpent intervall.
I det tredje intervallet er tallet 1 ikke med, mens tallet 3 er med. I det fjerde er tallet 1 med, mens 3 ikke er med. De to siste intervallene kalles halvåpne intervaller.
Intervallet inneholder alle reelle tall større enn eller lik .
Intervallet inneholder alle reelle tall mindre enn .
Forklar hva som er forskjellen på et lukket, et åpent og et halvåpent intervall.