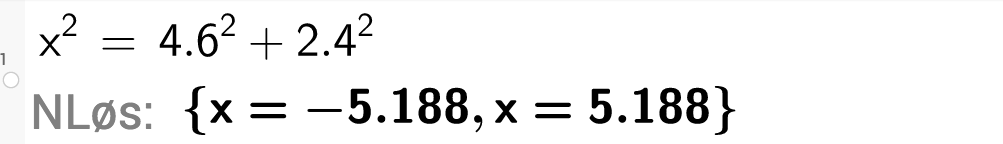Pytagoras’ setning
Tegn en trekant som er rettvinklet og der de korteste sidene er tre og fire enheter lange. Figuren viser en slik trekant som er tegnet i GeoGebra. Mål den lengste sida. Blir denne fem enheter lang?
Ta nå alle de tre sidelengdene og multipliser dem med seg selv. Du får da kvadratet av sidelengdene.
Kvadratet av sidelengden er
Kvadratet av sidelengden
Kvadratet av sidelengden
Sammenlign summen av kvadratene til de to korteste sidene med kvadratet til den lengste sida. Hva ser du?
Vi ser at
Det viser seg at denne sammenhengen gjelder for alle trekanter som har en vinkel på 90°.
For å kunne formulere denne sammenhengen med ord gir vi navn på sidene i rettvinklede trekanter.
Den lengste sida i en rettvinklet trekant kaller vi hypotenus. De to korteste sidene kaller vi kateter.
Pytagoras' setning:
Legg merke til navnsettingen. Vi bruker store bokstaver som navn på punkter eller hjørner i trekanten. Små bokstaver brukes som navn og måltall for sidelengdene. Det er vanlig at vi har den samme bokstaven på motstående hjørner og sider.
Lag et kvadrat med sidelengder
Del sidelengdene i to deler
Det grå arealet er et kvadrat (hvorfor?) med sidelengde
Flytt på trekantene inne i det store kvadratet som vist på neste figur. (I GeoGebra lager du en ny tegning. Bruk rutenett.)
Arealet av de to store kvadratene er like store da sidelengdene er lik
Samlet areal til de fire rettvinklede trekantene er like store i begge figurene.
Det må bety at de grå arealene i de to figurene er like store, altså at
Eksempel 1. Hypotenusen er ukjent
Vi ønsker å finne ut hvor lang sida
Sida
Eksempel 2. Kateten er ukjent
Vi ser nå på den neste trekanten. Denne gangen velger vi å bruke CAS for å finne den ukjente sida ved hjelp av Pytagoras' setning:
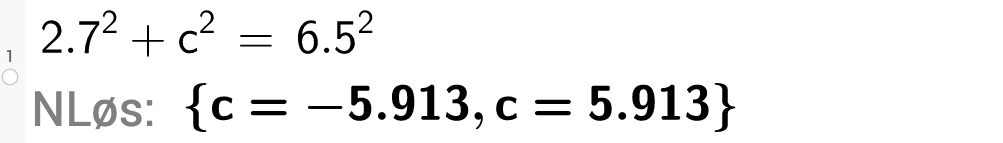
Sida
Eksempel 3. Et praktisk eksempel
En stige skal plasseres 2,4 meter fra en husvegg slik at den akkurat når opp til vinduskarmen i et vindu i andre etasje. Vinduskarmen er 4,6 meter over bakken.
Hvor lang må stigen være?
Her kan du se en video som viser hvordan man kan bruke Pytagoras' setning i praksis når man skal lage rette vinkler.
Se videoen, og etterpå kan du kanskje bruke noe av det du lærte til å sjekke om hjørnene i klasserommet ditt eller i stua hjemme er rette? Alt du trenger, er en tommestokk eller et målebånd!