Omdreiingslekamar
Dersom vi dreier grafen til ein funksjon 360° om -aksen, vil grafen forme eit tredimensjonalt objekt som vi kallar omdreiingslekam. Forma på ein omdreiingslekam avheng av forma på grafen, men alle omdreiingslekamar vil ha til felles at dei har perfekt symmetri om -aksen.
Dersom grafen til dømes er ei rett linje, blir omdreiingslekamen ei kjegle eller ei avkorta kjegle. På biletet under har vi lagt inn ein rettlinja graf frå
Du kan dra i det tredimensjonale grafikkfeltet på figuren over for å sjå kjegla frå ulike synsvinklar. Du kan òg få figuren til å rotere av seg sjølv ved å dra i grafikkfeltet med musepeikaren og så sleppe museknappen. Du kan nullstille figuren med knappen med dei runde pilene.
Filer
Ei anna moglegheit er at grafen har bogeform, som til dømes grafen til
Filer
Kva får vi dersom vi dreier ei linje som er parallell med
Kva form vil omdreiingslekamen få dersom vi dreier ein halvsirkel 360° om diameteren?
Vi kan teikne omdreiingslekamar i 3D-grafikkfeltet i GeoGebra, og vi skal vise metoden ved hjelp av funksjonen
For å få teikna ein omdreiingslekam i 3D-grafikkfeltet i GeoGebra må vi bruke nokre samanhengar knytte til parameterframstilling. Dette skal vi sjå nærare på i emnet Vektorar og parameterframstillingar i rommet, men "oppskrifta" er mogleg å bruke allereie no.
Først må vi vise 3D-grafikkfeltet ved å gå til menyvalet "Vis" i hovudmenyen til GeoGebra. Vi definerer så funksjonen
Overflate(u,f(u)sin(t),f(u)cos(t),u,1,10,t,0,2pi)
urepresenterer i denne samanhengen den variable i funksjonen, i dette tilfellet er dettex ter variabel for omdreiinga, som blir angitt i radianar.f(u)sin(t),f(u)cos(t)representerer koordinatane angitt på parameterform.u,1,10angir definisjonsområdet tilu(og dermed tilx t,0,2piangir ei omdreiing frå0 2 π
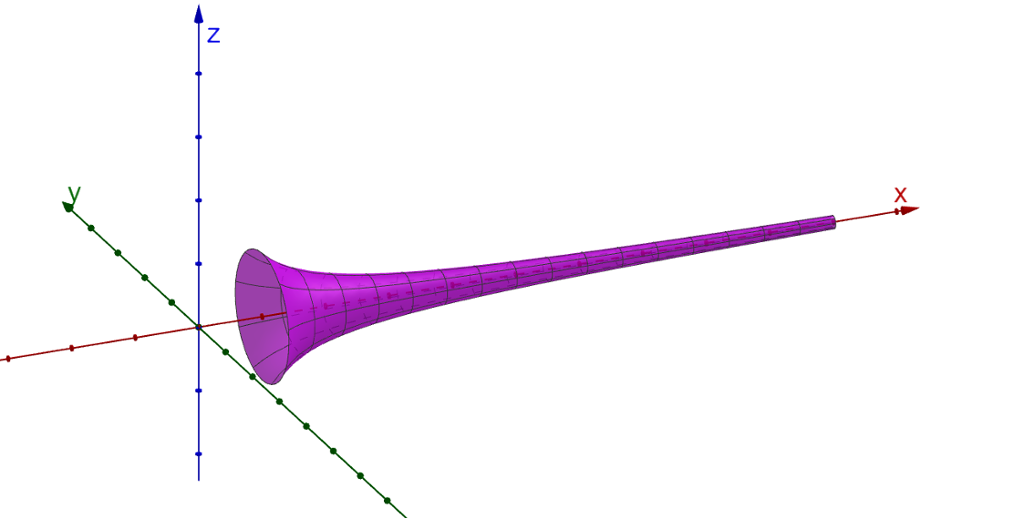
Korleis kan du lage større "tut" på Gabriels horn, det vil seie større diameter på opninga til venstre på biletet over?
Det er mogleg å bruke ei forenkling for å teikne omdreiingslekamar i 3D-grafikkfeltet i GeoGebra. Dersom vi skal bruke denne forenklinga, føreset vi at funksjonen er angitt med den definisjonsmengda som vi ønsker å gjere rotasjonen for, og at omdreiinga startar frå
Dersom vi bruker den forenkla formelen for å teikne Gabriels horn, vil vi måtte skrive følgande i algebrafeltet:
Overflate(f,2pi,xAkse)
Som nemnt over må funksjonen
Vi kan òg angi rotasjon om dei andre to aksa ved å skrive yAkse og zAkse i staden for xAkse.
Vi kan òg lage ein omdreiingslekam ved å dreie eit område mellom to grafar. I dømet under har vi to funksjonar,
Filer
For å teikne ein omdreiingslekam som kjem fram ved omdreiing av eit område i 3D-grafikkfeltet i GeoGebra, angir vi overflatene kvar for seg.
For å få teikna omdreiingslekamen som er vist i dømet over, vil grenseverdiane vere skjeringspunkta, og vi skriv følgande i algebrafeltet i GeoGebra:
Overflate(u,f(u)sin(t),f(u)cos(t),u,-1,1,t,0,2pi)
Overflate(v,g(v)sin(t),g(v)cos(t),v,-1,1,t,0,2pi)
Merk at vi må bruke ulike variablar (u og v) for funksjonane.
La
Dersom vi tenker at vi lagar vertikale (loddrette) snitt i ein slik omdreiingslekam, vil snittflatene vere perfekte sirklar, der radius avheng av kvar i figuren vi lagar snittet.
Radius i ein slik snittsirkel vil vere avstanden frå
Vi har då følgande samanheng:
Arealet av ein snittsirkel blir ut frå dette
For å kunne berekne volumet av omdreiingslekamen som kjem fram ved omdreiing av grafen til
Vi har berekna volum av romfigurar tidlegare, i fagartikkelen "Volum og bogelengde", og der kom vi fram til at eit uttrykk for det totale volumet er
der
Sidan vi har funne at arealet av ei sirkelforma skive er
Korleis kan vi berekne volum av ein omdreiingslekam som kjem fram ved omdreiing av eit område mellom to grafar?