Måleiningar for areal
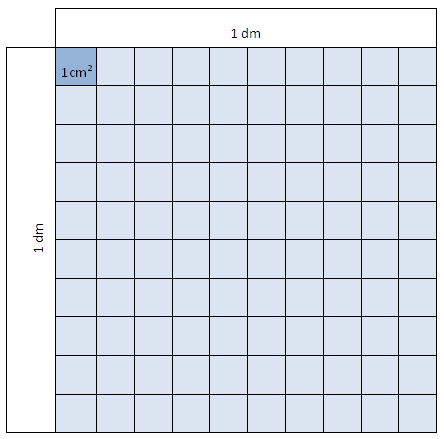
Vi definerer éin kvadratdesimeter, 1 dm2, som arealet, eller flateinnhaldet, til eit kvadrat med sidelengder på 1 dm.
Eit kvadrat med sider 1 cm har eit areal på éin kvadratcentimeter, 1 cm2.
Tilsvarande definerer vi areal på 1 m2, 1 mm2 og så vidare.
Figuren viser at det er 100 cm2 i 1 dm2. Det betyr igjen at
På same måte er det plass til 100 mm2 i 1 cm2 og 100 dm2 i 1 m2.
Akkurat som for lengde har det vore mange måleiningar for areal i bruk. Nokre av dei bruker vi framleis, som til dømes eit dekar. Det kallar vi òg eit mål, og det blir brukt om tomtestorleikar. Eit dekar svarer til 1 000 kvadratmeter. Dekar betyr 10 ar, og ar svarer til 100 kvadratmeter. Eit hektar er 10 dekar, eller 100 ar.
Vi hugsar samanhengen mellom måleiningar for lengde og set opp ein tilsvarande tabell for arealsamanhengane:
måleining | forkorting | talet på kvadratmeter |
|---|---|---|
kvadratkilometer | 1 000 000 | |
hektar | ha | 10 000 |
dekar | daa | 1 000 |
ar | a | 100 |
kvadratmeter | 1 | |
kvadratdesimeter | 0,01 | |
kvadratcentimeter | 0,000 1 | |
kvadratmillimeter | 0,000 001 |
På same måte som med lengde treng vi å kunne gjere om mellom ulike einingar, men som vi såg over, er det her plass til 100 cm2 i 1 dm2. Då må vi gonge med eller dele på 100 når vi gjer om.
Døme
Vi ser at det raskt blir ganske mange siffer.
Når vi set opp måleiningane for areal etter kvarandre, som i tabellen nedanfor, kan vi ha som hugseregel at vi må gonge med 100 når vi går éin plass til høgre i tabellen (vi flyttar kommaet to plassar til høgre), og vi må dele med 100 når vi går éin plass til venstre (vi flyttar kommaet to plassar til venstre).
0,000 002 3 | 0,000 23 | 0,023 | 2,3 | 230 | 23 000 | 2 300 000 |
0,000 000 45 | 0,000 045 | 0,004 5 | 0,45 | 45 | 4 500 | 450 000 |
Legg merke til at vi ikkje har teke med dekar i denne tabellen. Kvifor har vi ikkje det, trur du?
Når vi jobbar med areal, må vi òg ta omsyn til kor presise målingar vi har gjort. Det er alltid den minst nøyaktige målinga som styrer kor nøyaktig vi skal vere i svaret. Vi ser på eit døme der vi reknar ut arealet av eit rektangel.
Vi reknar ut arealet på vanleg måte:
Når vi skal avgjere kor mykje vi skal runde av, bruker vi som hovudregel like mange gjeldande siffer i svaret som i det måltalet med færrast gjeldande siffer. Vi definerer gjeldande siffer som alle siffer i talet sett bort frå nullar først i talet. Det betyr at 0,000 005 har eitt gjeldande siffer, mens 500 000 har seks gjeldande siffer.
Det betyr at vi må runde av arealet vårt til 24 cm2, sidan høgda i rektangelet har berre to gjeldande siffer.
Det er vanleg å bruke minst to gjeldande siffer sjølv om eitt av måltala berre har eitt siffer. Det er òg sånn at svaret av og til får automatisk fleire gjeldande siffer enn alle måltala (prøv til dømes å rekne ut arealet av eit kvadrat med sidelengde 20). Vi bruker sunn fornuft i praktiske døme. Reglane for bruk av gjeldande siffer er mykje strengare i fag som til dømes fysikk.
Når vi legg saman ulike areal, tel vi ikkje gjeldande siffer, men ser på nøyaktigheita i målingane slik som når vi reknar med lengder. Ein hugseregel er å bruke eit likt tal på desimalar som det måltalet med færrast desimalar. Hugs på at storleikane må ha lik måleining!