Binomisk sannsynsmodell

Du skal ha matteprøve. Du er ikkje førebudd, og alle svaralternativa verkar like sannsynlege. Vi går ut frå at dei ulike oppgåvene er uavhengige av kvarandre. Det vil seie at kva du svarer på éi oppgåve, ikkje påverkar svaret på den neste.

Du kryssar av heilt tilfeldig. Sannsynet for å svare riktig på ei oppgåve er då $\frac{1}{4}$, og sannsynet for å svare feil er $\frac{3}{4}$.

Kva er sannsynet for å få null, eitt, to, tre og fire riktige svar?

Det er berre éin måte du kan få fire riktige svar på. Vi lar $R$ stå for at svaret er riktig, og $G$ stå for at svaret er feil.

$\begin{array}{rcl}P\left(RRRR\right)& = & P(R_1\cap R_2\cap R_3\cap R_4)\\ & & \\ & =& P\left(R_1\right)·P\left(R_2\right)·P\left(R_3\right)·P\left(R_4\right)\\ & & \\ & =& \frac{1}{4}·\frac{1}{4}·\frac{1}{4}·\frac{1}{4}={\left(\frac{1}{4}\right)}^4\end{array}$

Det er òg berre éin måte du kan få null riktige svar på.

$P\left(GGGG\right)=\frac{3}{4}·\frac{3}{4}·\frac{3}{4}·\frac{3}{4}={\left(\frac{3}{4}\right)}^4$

Men på kor mange måtar kan du få to riktige svar?

Sannsynet for å svare riktig på dei to første oppgåvene (og feil på dei to neste) er

$P\left(RRGG\right)=\frac{1}{4}·\frac{1}{4}·\frac{3}{4}·\frac{3}{4}={\left(\frac{1}{4}\right)}^2·{\left(\frac{3}{4}\right)}^2$

Men det er fleire måtar å få to riktige svar på. Du kan til dømes svare riktig på dei to siste oppgåvene ($GGRR$), på første og siste oppgåve ($RGGR$) og så vidare.

For å telje opp kor mange måtar det er, kan du lage eit valtre. Vi startar øvst på midten. For den første oppgåva teiknar vi to strekar på skrå nedover i kvar si retning. Den eine streken er for riktig svar, den andre for feil svar – altså éin strek for kvart val. Vi skriv òg på sannsynet for kvart enkelt val ved sida av valet.

Frå enden på kvart av desse to vala teiknar vi to nye strekar for den andre oppgåva, for riktig og for feil svar. No vil talet på strekar doble seg for kvar ny oppgåve, og vi får ein trestruktur. Etter fire oppgåver vil vi ha $2^4=16$ greiner på valtreet.

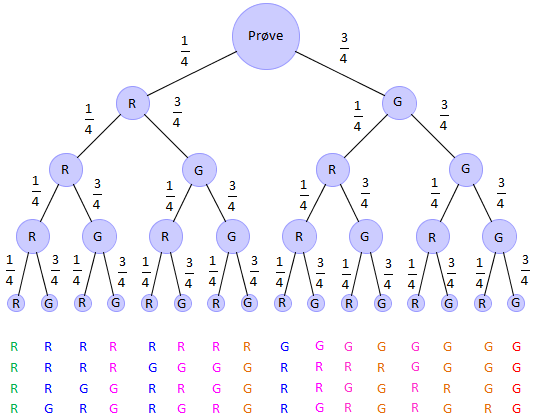
Valtreet over viser kor mange måtar du kan få null, eitt, to, tre og fire riktige svar på. Vi tel opp og samlar resultata i ein tabell.

Legg merke til at dette er fjerde rad i Pascals trekant.

At binomialkoeffisientane dukkar opp her, er ikkje så underleg. Å finne talet på kor mange måtar vi kan få to rette svar på, er det same som å finne ut på kor mange måtar vi kan velje to plassar av fire der det skal stå $R$.

Vi legg merke til at alle stiane gjennom valtreet som gir to riktige svar, har likt sannsyn, nemleg $$ {\left(\frac{1}{4}\right)}^2·{\left(\frac{3}{4}\right)}^2$$

På sida Tre ulike typar utval kan du sjå at vi kan bruke binomialkoeffisienter for å rekne ut talet på kombinasjonar ved denne typen utval. Vi får altså at

$P\left(\mathrm{To} \mathrm{riktige} \mathrm{svar}\right)=\left(\begin{array}{c}4\\ 2\end{array}\right)·{\left(\frac{1}{4}\right)}^2·{\left(\frac{3}{4}\right)}^2$

På same måte vil då

$P\left(\mathrm{Tre} \mathrm{riktige} \mathrm{svar}\right)=\left(\begin{array}{c}4\\ 3\end{array}\right)·{\left(\frac{1}{4}\right)}^3·{\left(\frac{3}{4}\right)}^1$

Samansette forsøk som dette kallar vi binomiske forsøk. Talet på rette svar er ein stokastisk variabel. I vårt døme kan denne variabelen ha verdien 0, 1, 2, 3 eller 4. Vi kan då skrive eit generelt uttrykk for sannsynsfordelinga slik:

$$ P\left(X=k\right)=\left(\begin{array}{c}4\\ k\end{array}\right)·{\left(\frac{1}{4}\right)}^k·{\left(\frac{3}{4}\right)}^{4-k}$$

Her er $$ X$$ den stokastiske variabelen, og $$ k$$ er talet på rette. Vi legg merke til at sannsynet for å ikkje få rett svar må opphøgjast i talet på spørsmål som står att når vi har «teke ut» dei svara som er riktige.

Dette gjeld heilt generelt. Vi går ut frå at vi har ei prøve med $n$ oppgåver som blir svarte på heilt uavhengig av kvarandre. For kvar oppgåve er det to moglegheiter: Anten svarer vi riktig, eller så svarer vi feil.

Alle oppgåvene har like mange svaralternativ, derfor er sannsynet for å svare riktig likt heile tida. Vi kan kalle dette sannsynet for $$ p$$. Då blir sannsynet for å svare feil på ei oppgåve likt $$ 1-p$$.

Talet på riktige svar er den stokastiske variabelen $$ X$$. Då får vi ein generell formel som kan brukast for å rekne ut sannsynet for at $$ X$$ har verdien $$ k$$:

$$ P\left(X=k\right)=\left(\begin{array}{c}n\\ k\end{array}\right)·{\left(p\right)}^k·{\left(1-p\right)}^{n-k}$$

Andre døme på binomiske forsøk

Å kaste ein terning eit bestemt tal gonger og sjå om vi får seksar eller ikkje på kvart enkelt kast, er eit anna døme på eit binomisk forsøk. Vi kan bruke formelen ovanfor til å berekne sannsynet for å få eit bestemt tal seksarar.

Å kaste ein mynt eit bestemt tal gonger og sjå om vi får «krone» eller «mynt» på kvart enkelt kast, er òg eit døme på eit binomisk forsøk. Vi kan bruke formelen ovanfor til å berekne sannsynet for å få eit bestemt tal «krone».

Begge desse døma skal du få prøve deg på i oppgåvene seinare.

Vi kan bruke sannsynskalkulatoren i GeoGebra til å rekne ut binomisk sannsyn.

Ei fleirvalsprøve har fem oppgåver med fire svaralternativ på kvar oppgåve. Du svarer på fleirvalsprøva ved rein gjetting.

Først ser vi på korleis du kan finne sannsynet for å svare riktig på akkurat éi av oppgåvene. Du vel «Binomisk fordeling» og fyller inn som vist nedanfor.

Så ser vi korleis du kan finne sannsynet for å få meir enn to riktige svar:

Vi kan importere binom frå scipy.stats. Her har vi ein metode binom.pmf() som gir oss den binomiske fordelinga. Metoden har tre argument. Det første argumentet er ei liste over dei verdiane av den stokastiske variabelen vi ønskjer å finne sannsynet for. Dei to neste er $$ n$$, talet på forsøk, og $$ p$$, sannsynet for suksess. Vi lagar eit program for å skrive ut sannsynsfordelinga i forsøket vi gjorde med fem spørsmål og fire svaralternativ:

1from scipy.stats import binom
2
3n = 5
4p = 0.25
5X = []                       #lagar ei liste med verdiane til den stokastiske variabelen
6
7for i in range(n+1): 
8    X.append(i)              #legg inn alle dei moglege verdiane til X
9
10rettesvar = binom.pmf(X,n,p) #lagar ein array med sannsynsfordelinga
11
12for i in rettesvar:
13    print(i)                 #skriv sannsynsfordelinga i ein kolonne

Om vi ikkje ønskjer heile fordelinga, men til dømes ønskjer å finne sannsynet for å få to eller tre rette svar, set vi inn lista [2,3] som første argument i binom.pmf(). Vi kan òg bruke metoden sum() for å finne det samla sannsynet.

1
2from scipy.stats import binom
3
4n = 5
5p = 0.25
6
7rettesvar = binom.pmf([2,3],n,p)
8
9for i in rettesvar:
10    print(i) 
11
12print(sum(rettesvar))             #vi finn summen av sannsyna for 2 og 3

Kopier programma til editoren din, og køyr dei!