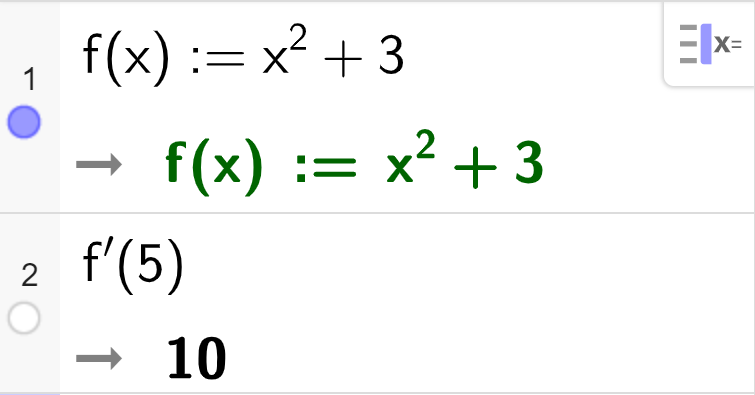Definisjonen av den deriverte f ' x = lim Δ x → 0 f x + Δ x - f x Δ x
a) Bruk definisjonen av den deriverte til å bestemme den deriverte av funksjonen
f x = 3
Løsning f x + ∆ x = 3 f ' x = lim Δ x → 0 f x + Δ x - f x Δ x = lim Δ x → 0 3 - 3 Δ x = lim Δ x → 0 0 Δ x = 0
b) Bruk definisjonen av den deriverte til å bestemme den deriverte av funksjonen
f x = k
Løsning f x + ∆ x = k f ' x = lim Δ x → 0 f x + Δ x - f x Δ x = lim Δ x → 0 k - k Δ x = lim Δ x → 0 0 Δ x = 0
For hver av oppgavene under skal du bruke definisjonen av den deriverte til å bestemme den deriverte i punktet x = 2 x = 2
a) f x = x
Løsning f 2 = 2 f 2 + ∆ x = 2 + ∆ x f ' 2 = lim Δ x → 0 f 2 + Δ x - f 2 Δ x = lim Δ x → 0 2 + ∆ x - 2 Δ x = lim Δ x → 0 ∆ x Δ x = lim Δ x → 0 1 = 1
At den deriverte er lik 1, betyr at stigningen i punktet x = 2 1 x = 2 1 x = 2 1
b) f x = 3 x
Løsning f 2 = 3 · 2 = 6 f 2 + ∆ x = 3 ( 2 + ∆ x ) = 6 + 3 ∆ x f ' 2 = lim Δ x → 0 f 2 + Δ x - f 2 Δ x = lim Δ x → 0 6 + 3 ∆ x - 6 Δ x = lim Δ x → 0 3 ∆ x Δ x = lim Δ x → 0 3 = 3
Stigningen i punktet x = 2 3 x = 2 3 x =2 3
Siden vi vet at grafen er ei rett linje, ser vi at stigningstallet er lik 3.
c) f x = x 2
Løsning f 2 = 2 2 = 4 f 2 + ∆ x = 2 + ∆ x 2 = 4 + 4 ∆ x + ∆ x 2 f ' 2 = lim Δ x → 0 f 2 + Δ x - f 2 Δ x = lim Δ x → 0 4 + 4 ∆ x + ∆ x 2 - 4 Δ x = lim Δ x → 0 4 ∆ x + ∆ x 2 Δ x = lim Δ x → 0 4 + ∆ x = 4
Stigningen i punktet x = 2 4 x = 2 4 x = 2 4
d) f x = 2 x 2 + 4
Løsning f 2 = 2 · 2 2 + 4 = 12 f 2 + ∆ x = 2 2 + ∆ x 2 + 4 = 2 ( 2 2 + 2 · 2 · ∆ x + ( ∆ x ) 2 ) + 4 = 12 + 8 ∆ x + 2 ( ∆ x ) 2 f ' 2 = lim Δ x → 0 f 2 + Δ x - f 2 Δ x = lim Δ x → 0 12 + 8 ∆ x + 2 ( ∆ x ) 2 - 12 Δ x = lim Δ x → 0 12 + 8 ∆ x + 2 ∆ x 2 + 12 Δ x = lim Δ x → 0 8 ∆ x + 2 ( ∆ x ) 2 Δ x = lim Δ x → 0 ∆ x 8 + 2 ∆ x Δ x = 8
Stigningen i punktet x = 2 8 x = 2 8 x = 2 8
a) Bruk definisjonen av den deriverte til å bestemme den deriverte til den generelle førstegradsfunksjonen.
Løsning Den generelle førstegradsfunksjonen er f x = a x + b .
f x + ∆ x = a x + ∆ x + b = a x + a ∆ x + b f ' x = lim Δ x → 0 f x + ∆ x - f x Δ x = lim Δ x → 0 a x + a ∆ x + b - a x + b Δ x = lim Δ x → 0 a x + a ∆ x + b - a x - b Δ x = lim Δ x → 0 a ∆ x Δ x = lim Δ x → 0 a = a
b) Bruk definisjonen av den deriverte til å bestemme den deriverte til den generelle andregradsfunksjonen.
Løsning Den generelle andregradsfunksjonen:
f x = a x 2 + b x + c
f x + ∆ x = a x + ∆ x 2 + b x + ∆ x + c = a x 2 + 2 x ∆ x + ∆ x 2 + b x + b ∆ x + c = a x 2 + 2 a x ∆ x + a ∆ x 2 + b x + b ∆ x + c f ' x = lim Δ x → 0 f x + Δ x - f x Δ x = lim Δ x → 0 a x 2 + 2 a x ∆ x + a ∆ x 2 + b x + b ∆ x + c - a x 2 + b x + c Δ x = lim Δ x → 0 2 a x ∆ x + a ∆ x 2 + b ∆ x Δ x = lim Δ x → 0 2 a x ∆ x + a ∆ x 2 + b ∆ x Δ x = lim Δ x → 0 2 a x + a ∆ x + b = 2 a x + b
Bruk definisjonen av den deriverte til å bestemme den deriverte.
a) g x = 1 x
Løsning f x + ∆ x = 1 x + ∆ x f ' x = lim Δ x → 0 f x + Δ x - f x Δ x = lim Δ x → 0 1 x + ∆ x - 1 x Δ x = lim Δ x → 0 1 · x ( x + ∆ x ) · x - 1 · ( x + ∆ x ) x ( x + ∆ x ) Δ x = lim Δ x → 0 x - ( x + ∆ x ) x ( x + ∆ x ) Δ x = lim Δ x → 0 x - x - ∆ x x ( x + ∆ x ) Δ x = lim Δ x → 0 ∆ x x ( x + ∆ x ) Δ x = lim Δ x → 0 - ∆ x x ( x + ∆ x ) · 1 ∆ x = lim Δ x → 0 - ∆ x x x + ∆ x ∆ x = lim Δ x → 0 - ∆ x x x + ∆ x ∆ x = lim Δ x → 0 - 1 x 2 + x ∆ x = - 1 x 2
b) h x = 1 x - 1
Løsning f x + ∆ x = 1 x + ∆ x - 1 f ' x = lim Δ x → 0 f x + Δ x - f x Δ x = lim Δ x → 0 1 x + ∆ x - 1 - 1 x - 1 Δ x = lim Δ x → 0 1 x + ∆ x - 1 - 1 x - 1 · 1 ∆ x = lim Δ x → 0 x - 1 - x + ∆ x - 1 x + ∆ x - 1 · x - 1 · 1 ∆ x = lim Δ x → 0 x - 1 - x - ∆ x + 1 x + ∆ x - 1 · x - 1 · 1 ∆ x = lim Δ x → 0 - ∆ x x + ∆ x - 1 · x - 1 · 1 ∆ x = lim Δ x → 0 - ∆ x x + ∆ x - 1 · x - 1 · 1 ∆ x = - 1 x - 1 2
a) Bruk definisjonen av den deriverte til å bestemme den momentane vekstfarten til f x = x 2 + 3 x = 5
Løsning f 5 = 5 2 + 3 = 28 f 5 + ∆ x = 5 + ∆ x 2 + 3 = 5 2 + 2 · 5 ∆ x + ∆ x 2 + 3 = 28 + 10 ∆ x + ∆ x 2 f ' 5 = lim Δ x → 0 f x + Δ x - f x Δ x = lim Δ x → 0 28 + 10 ∆ x + ∆ x 2 - 28 Δ x = lim Δ x → 0 28 + 10 ∆ x + ∆ x 2 + 28 ∆ x = lim Δ x → 0 10 ∆ x + ∆ x 2 ∆ x = lim Δ x → 0 10 + ∆ x = 10
b) Bruk digitale verktøy til å bestemme den momentane vekstfarten til f x = x 2 + 3 x = 5
Løsning Vi løser i GeoGebra: