Forenkling av rasjonale uttrykk
Husker du at et tall som kan skrives som en brøk med hele tall i telleren og nevneren, kalles et rasjonalt tall?
På samme måte er et typisk rasjonalt uttrykk en brøk med bokstavuttrykk i telleren og i nevneren.
Du kan bruke de regnereglene du nå har lært, til å forenkle og trekke sammen rasjonale uttrykk. Regnereglene for brøkregning gjelder selvfølgelig også om du erstatter tall med bokstaver.
Vi ønsker å skrive et rasjonalt uttrykk så enkelt som mulig. For å få til dette vil vi faktorisere telleren og nevneren, for så å undersøke om vi kan forkorte bort noen faktorer. Vi viser hvordan vi går fram ved hjelp av et eksempel:
Vi skal forkorte uttrykket .
🤔 Tenk over: Vi ser at vi har flere ledd både i telleren og i nevneren. Hvorfor sier vi likevel at dette er et enleddet uttrykk?
Vi starter med å faktorisere telleren og nevneren hver for seg:
Vi kan nå skrive om det opprinnelige uttrykket. Vi forkorter de faktorene som forekommer både i telleren og i nevneren og får
Ofte må vi trekke sammen uttrykk før vi kan forkorte dem. Dette gjelder dersom vi har flere ledd. Vi viser også dette med et eksempel.
Vi skal trekke sammen uttrykket
Det første vi må gjøre, er å få satt uttrykket på en felles brøkstrek. Da må vi finne den minste fellesnevneren. Det gjør vi ved å faktorisere begge nevnerne. Nevneren i det andre leddet her er allerede lineær og kan ikke faktoriseres mer, mens nevneren i det første leddet kan faktoriseres ved hjelp av konjugatsetningen:
Vi legger merke til at nevneren i andre ledd er lik en av faktorene i nevneren i første ledd. Fellesnevneren til de to brøkene blir derfor
Til slutt faktoriserer vi telleren og forkorter faktor mot faktor der dette er mulig:
Trinnvis framgangsmåte
Vi faktoriserer nevnerne for å finne fellesnevneren.
Vi utvider brøkene slik at alle brøkene har lik nevner.
Vi leddene setter på en felles brøkstrek og regner ut telleren.
Vi faktoriserer telleren.
Vi forkorter faktorene som er like i telleren og nevneren.
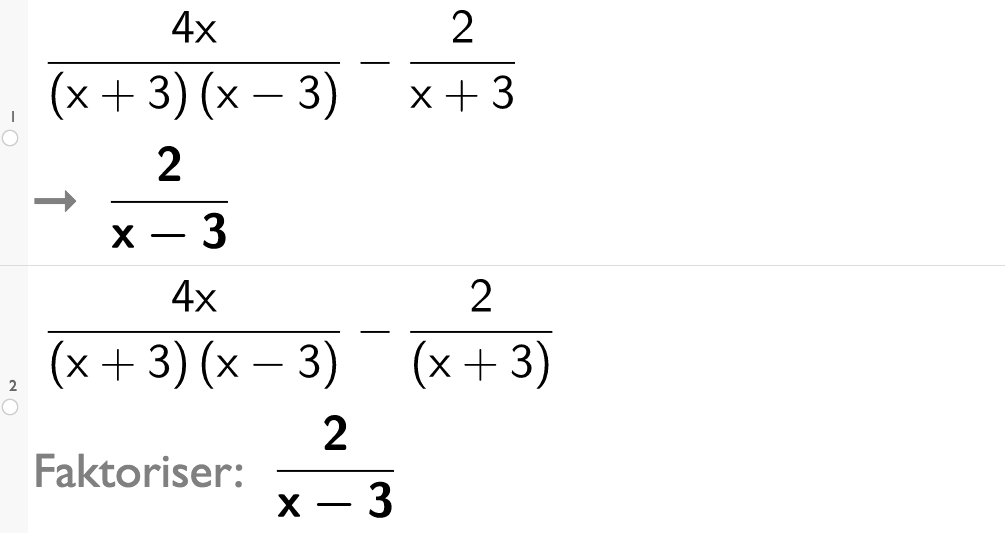
I GeoGebra skriver vi inn uttrykket og trykker enter eller velger verktøyknappen for faktorisering, den fjerde knappen fra venstre.
Du kan også bruke kommandoen "Faktoriser(uttrykket)".