Fágaartihkal

En sirkel i planet

En sirkel kan uttrykkes ved en likning. For å finne denne likningen bruker vi vektorer.

Likningen for en sirkel

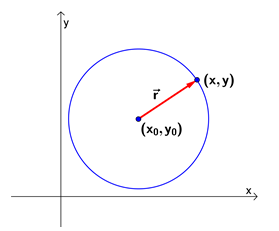
Sirkel i planet. — Govva: Stein Aanensen, Olav Kristensen / CC BY-SA 4.0

Til høyre ser du en sirkel med sentrum i punktet $(x_{0}, y_{0})$ . Vi setter radius i sirkelen lik $r$ . Sirkelen er samlingen av, eller det geometriske stedet for, alle punkter $(x, y)$ som har avstanden $r$ fra punktet $(x_{0}, y_{0})$ .

Vi lar $\vec{r}$ være vektoren fra sentrum i sirkelen, $(x_{0}, y_{0})$ , til et vilkårlig punkt på sirkelen, $(x, y)$ .

$\vec{r} = [x - x_{0}, y - y_{0}]$

Da er $|\vec{r}| = r$ .

Dette gir

$\begin{array}{rcl} |\vec{r}| & = & r \\ |[x - x_{0}, y - y_{0}]| & = & r \\ \sqrt{{(x - x_{0})}^{2} + {(y - y_{0})}^{2}} & = & r \\ {(x - x_{0})}^{2} + {(y - y_{0})}^{2} & = & r^{2} \end{array}$

Setning

Likningen for en sirkel med sentrum i $(x_{0}, y_{0})$ og med radius lik r kan skrives på formen

$\begin{matrix} \begin{matrix} \begin{array}{clc} \begin{array}{rcl} \end{array} \begin{array}{rcl} (x - x_{0}) \end{array} \begin{array}{rcl} ^{2} \end{array} \begin{array}{rcl} + \end{array} \begin{array}{rcl} (y - y_{0}) \end{array} \begin{array}{rcl} ^{2} \end{array} \begin{array}{rcl} = \end{array} \begin{array}{rcl} r \end{array} \begin{array}{rcl} ^{2} \end{array} \end{array} \end{matrix} \end{matrix}$

Legg merke til at en sirkel per definisjon bare er samlingen av punkter som har avstand r fra sentrum.

Noen ganger blir imidlertid begrepet «sirkel» brukt om hele området som er avgrenset av denne samlingen av punkter. Vi snakker for eksempel om «arealet av en sirkel». Punktene som har avstanden r fra sentrum, kalles da «sirkelperiferien».

Eksempel 1

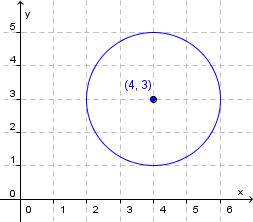
Sirkel i planet. Illustrasjon. — Govva: Stein Aanensen, Olav Kristensen / CC BY-SA 4.0

Vi skal finne likningen for en sirkel som har sentrum i $(4, 3)$ og radius lik 2.

Her er $x_{0} = 4, y_{0} = 3 og r = 2$ .
Setningen ovenfor gir oss likningen for denne sirkelen
$\begin{array}{rcl} \end{array} \begin{array}{rcl} (x - 4) \end{array} \begin{array}{rcl} ^{2} \end{array} \begin{array}{rcl} + \end{array} \begin{array}{rcl} (y - 3) \end{array} \begin{array}{rcl} ^{2} \end{array} \begin{array}{rcl} = \end{array} \begin{array}{rcl} 4 \end{array}$

Eksempel 2

Vi skal bestemme sentrum og radius i en sirkel som er gitt ved ${(x - 2)}^{2} + {(y + 4)}^{2} = 5^{2}$ .

Hvis vi sammenlikner med likningen ${(x - x_{0})}^{2} + {(y - y_{0})}^{2} = r^{2}$ , ser vi at $x_{0} = 2$ , $y_{0} = - 4$ og $r = 5$ .

Sirkelen har sentrum i $(2, - 4)$ og $r = 5$ .

En sirkel har likningen $x^{2} + y^{2} = r^{2}$ . Hvor ligger sentrum i denne sirkelen?

Omforming av sirkellikning – fullstendige kvadraters metode

Vi har sett at likningen for en sirkel med sentrum i $(x_{0}, y_{0})$ og med radius lik r kan skrives på formen
${(x - x_{0})}^{2} + {(y - y_{0})}^{2} = r^{2}$

Vi kan regne ut venstresida slik:

$x^{2} - 2 x x_{0} + {x_{0}}^{2} + y^{2} - 2 y y_{0} + {y_{0}}^{2} = r^{2}$

Vi ser at vi får et uttrykk hvor både $x$ og $y$ er opphøyd i andre potens og har like koeffisienter. Dette er et krav som må være oppfylt for alle sirkellikninger. Vi ser at kravet er oppfylt for følgende likning:
$x^{2} + 2 x + y^{2} - 6 y = - 1$
Likningen kan derfor være en sirkellikning.

For å være helt sikre, og finne sentrum og radius i en eventuell sirkel, må vi skrive om likningen slik at vi får den på formen ${(x - x_{0})}^{2} + {(y - y_{0})}^{2} = r^{2}$ .

Uttrykkene ${(x - x_{0})}^{2}$ og ${(y - y_{0})}^{2}$ kalles fullstendige kvadrater.

I matematikk 1T lærte du å skrive om uttrykk for å lage fullstendige kvadrater. Nedenfor har vi tatt med to eksempler, men hvis du er usikker, kan du gå til sida Faktorisering av andregradsuttrykk ved å lage fullstendige kvadrater fra 1T og repetere dette skikkelig!

Husk at et fullstendig kvadrat er et andregradsuttrykk som kan faktoriseres ved hjelp av første eller andre kvadratsetning.

Eksempel 1

Vi skal undersøke om $x^{2} - 6 x + 9$ er et fullstendig kvadrat. Her er førstegradsleddet negativt. Vi må derfor prøve med andre kvadratsetning. Husker du hvordan andre kvadratsetning så ut?

Vis andre kvadratsetning

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

Vi må da sjekke om førstegradsleddet er «det dobbelte produkt», det vil si $2 a b$ .

Her er $2 a b = 2 \cdot x \cdot 3 = 6 x$ , altså lik førstegradsleddet i uttrykket $x^{2} - 6 x + 9$ .

Da er $x^{2} - 6 x + 9 = {(x - 3)}^{2}$ , og vi har et fullstendig kvadrat.

Eksempel 2

Vi skal legge til et konstantledd slik at uttrykket $x^{2} + 10 x$ blir et fullstendig kvadrat. Her er førstegradsleddet positivt. Vi må derfor bruke første kvadratsetning. Du kan klikke den fram under dersom du ikke husker hvordan den ser ut.

Vis første kvadratsetning

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Siden andregradsleddet er $x^{2}$ , må $a = \sqrt{x^{2}} = x$ .

«Det dobbelte produktet», $2 a b = 10 x$ .

Da er

$b = \frac{10 x}{2 a} = \frac{10 x}{2 x} = 5$

Vi får da at $b^{2} = 25$ , og det fullstendige kvadratet blir

$x^{2} + 10 x + 25 = {(x + 5)}^{2}$

For å lage fullstendig kvadrater sier vi ofte at vi må «halvere, kvadrere og addere». Ser du hva vi mener med det? Legg merke til at

$x^{2} + 10 x + 25 = x^{2} + 10 x + {(\frac{10}{2})}^{2}$

Sirkelen vår

Nå går vi tilbake til sirkelen gitt ved likningen

$x^{2} + 2 x + y^{2} - 6 y = - 1$

Vi sorterer leddene og legger til det vi mangler for å få fullstendige kvadrater.

$\begin{array}{rcl} x^{2} + 2 x + y^{2} - 6 y & = & - 1 \\ x^{2} + 2 x + {(\frac{2}{2})}^{2} + y^{2} - 6 y + {(\frac{6}{2})}^{2} & = & - 1 + {(\frac{2}{2})}^{2} + {(\frac{6}{2})}^{2} \\ x^{2} + 2 x + 1^{2} + y^{2} - 6 y + 3^{2} & = & - 1 + 1^{2} + 3^{2} \\ \underset{{(x + 1)}^{2}}{\underset{⏟}{x^{2} + 2 x + 1}} + \underset{{(y - 3)}^{2}}{\underset{⏟}{y^{2} - 6 y + 9}} & = & - 1 + 1 + 9 \\ {(x + 1)}^{2} + {(y - 3)}^{2} & = & 3^{2} \end{array}$

Legg merke til at vi legger til de samme leddene på begge sider av likhetstegnet!

Hvorfor må vi gjøre det?

Grafisk framstilling av sirkellikningen parentes x pluss 1 parentes slutt i andre minus parentes y minus 3 parentes slutt i andre er lik 9. Illustrasjon. — Govva: Stein Aanensen, Olav Kristensen / CC BY-SA 4.0

Dette er altså likningen for en sirkel med sentrum i $(- 1, 3)$ og radius $r = 3$ .

Likningen for en sirkel

Setning

Eksempel 1

Eksempel 2

Omforming av sirkellikning – fullstendige kvadraters metode

Eksempel 1

Eksempel 2

Sirkelen vår

Njuolggadusat teavstta geavaheapmái "En sirkel i planet"