Bevegelse. Fart og akselerasjon

En parameterframstilling for ei linje eller en kurve kan for eksempel bety posisjonen til en rakett som beveger seg langs linja eller kurven. Da står parameteren for tida. Vi kan da finne ut hvor raketten er til enhver tid ved å sette inn tidspunktet i parameterframstillingen. Vi skal også vise hvordan vi kan finne farten og akselerasjonen til en slik rakett ut ifra parameterframstillingen for posisjonen.

Figuren viser banen til en rakett som blir skutt opp. Raketten følger en bane gitt ved kurven .

er tida målt i sekunder etter oppskytingstidspunktet. Vi kan tenke oss at vi måler og i meter. Vi forutsetter at -planet er bakkenivå, og at -aksen peker loddrett oppover.

Tenk over

Hva blir den tilsvarende vektorfunksjonen til kurven ?

Aktuelle spørsmål å stille om raketten og banen den følger, er:

1. Hvor blir raketten skutt opp fra?

2. Hvor langt har raketten kommet etter 2 sekunder?

3. Hvor høyt har raketten kommet etter 2 sekunder?

4. Hvor fort går raketten da?

5. Hvor stor er akselerasjonen til raketten da?

Vi svarer på det første spørsmålet. Oppskytingstidspunktet er . Da har raketten posisjonen

Vi finner svaret på det andre spørsmålet ved først å sette inn i vektorfunksjonen. Da får vi at etter 2 sekunder har raketten posisjonen

Spørsmålet krever at vi svarer på hvor langt raketten har flyttet seg. Da må vi regne ut lengden av vektoren mellom de to posisjonene.

Høyden til raketten (spørsmål 3) blir det samme som -komponenten til . Vi har da forutsatt at -planet er vannrett. Fra utregningen av får vi derfor at raketten er 6 meter over bakken etter 2 sekunder.

De to siste spørsmålene venter vi litt med.

På figuren er rakettbanen tegnet som en stiplet kurve. og er to punkter i banen. Når raketten flytter seg fra til , endrer posisjonsvektoren seg fra til . Forflytningen blir derfor en vektor fra til .

Tenk over

Hva blir sammenhengen mellom de tre vektorene , og ?

Definisjon av fartsvektoren

I fysikkfaget definerer vi gjennomsnittsfarten ved en forflytning som delt på endringen i tid , det vil si den tida det tar å flytte seg fra til . Vi får

Legg merke til at vi ikke definerer gjennomsnittsfarten som banelengden, det vil si lengden av kurven i det aktuelle tidsrommet, delt på endringen i tid. Siden likningen er en vektorlikning, må vektoren for gjennomsnittsfart være parallell med .

Vi ønsker å komme fram til den momentane fartsvektoren i punktet . Da kan vi se for oss at vi flytter punktet nærmere og nærmere punktet . Jo nærmere punktet punktet er, jo bedre tilnærming får vi til momentanfarten. Det betyr at

Dette er definisjonen av den momentane fartsvektoren. Betraktningen er ganske lik det vi gjør i matematikk 1T der vi kommer fram til momentan vekstfart og den deriverte av en funksjon. Forskjellen er at vi nå har en vektor med tre komponenter, ikke en enkelt funksjon. Å ta denne grenseverdien betyr at vi skal la i hver av vektorkomponentene. Det betyr videre at for å finne fartsvektoren, skal vi derivere hver av vektorkomponentene med hensyn på .

Dersom , får vi derfor at

Tenk over

Hva kan vi si om retningen på i punktet ?

Banefart

Tenk over

Hvor fort går egentlig raketten?

Spørsmål 4 fra eksempelet

Nå kan vi svare på spørsmål 4 i raketteksempelet over. Når vi spør "Hvor fort går raketten etter 2 sekunder?", mener vi "Hvor stor er banefarten når ?".

Først må vi finne den momentane fartsvektoren. Siden , får vi

Raketten har farten etter 2 sekunder.

Tenk over

Hvorfor blir måleenheten for farten i eksempelet ?

Oppsummering: fart

Vi har en partikkel med posisjon gitt ved en vektorfunksjon

der parameteren står for tida. Da er den momentane fartsvektoren bestemt ved

Vi skriver også ofte

er i alle punkter parallell med tangenten til bevegelseskurven i punktet.

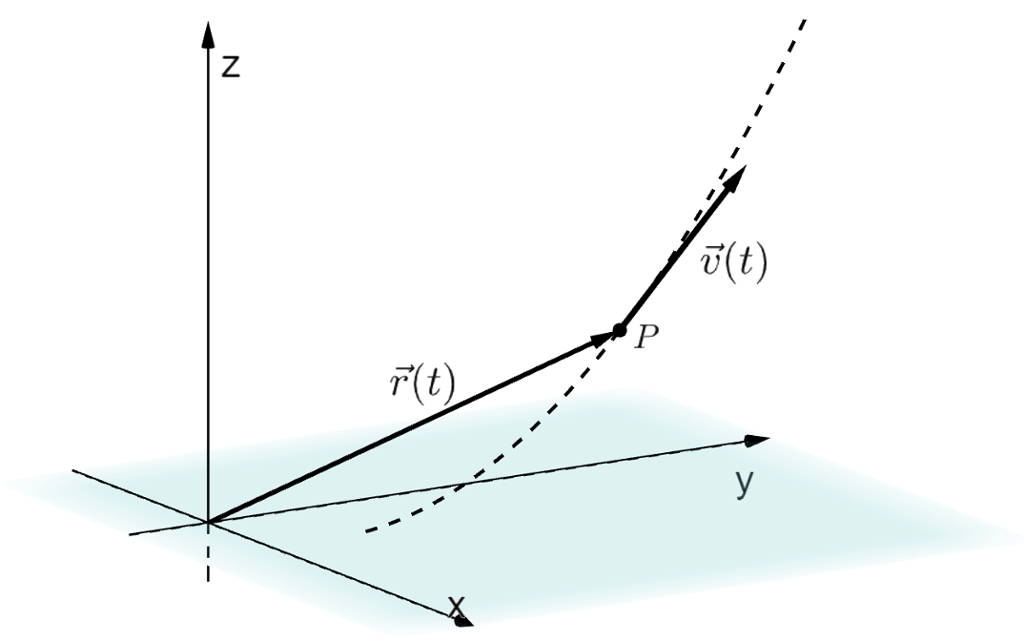
Banefarten er lengden av fartsvektoren, det vil si. Banefarten er den farten vi kan måle at partikkelen har uavhengig av retning.

Akselerasjon er et mål på hvor raskt farten endrer seg. Vi kan gjøre tilsvarende betraktning av fartsendringen som vi gjorde med posisjonsendringen over. Derfor er den momentane akselerasjonsvektoren i fysikken definert som

Dette gir oss videre at

Akselerasjonsvektoren er den deriverte av fartsvektoren og dermed den andrederiverte av posisjonsvektoren.

Når det i en oppgave spørres etter akselerasjonen, menes det vanligvis absoluttverdien av akselerasjonsvektoren, . I noen tilfeller kan det også spørres etter retningen på akselerasjonsvektoren.

Spørsmål 5 fra eksempelet

Nå kan vi svare på spørsmål 5 i raketteksempelet over. Når vi spør "Hvor stor er akselerasjonen til raketten etter 2 sekunder?", mener vi "Hvor stor er ?".

Først må vi finne akselerasjonsvektoren. Siden , får vi

Det betyr at akselerasjonen er konstant siden den ikke varierer med . Siden - og -komponentene er null, er akselerasjonen loddrett og lik etter 2 sekunder og til alle andre tidspunkter.

Tenk over

Hvorfor blir måleenheten for akselerasjonen i eksempelet ?