Rørsle. Fart og akselerasjon

Ei parameterframstilling for ei linje eller ei kurve kan til dømes bety posisjonen til ein rakett som beveger seg langs linja eller kurva. Då står parameteren $t$ for tida. Vi kan då finne ut kvar raketten er til eit gitt tidspunkt ved å setje inn tidspunktet i parameterframstillinga. Vi skal òg vise korleis vi kan finne farten og akselerasjonen til ein slik rakett ut ifrå parameterframstillinga for posisjonen.

Døme: rakett som blir skoten opp

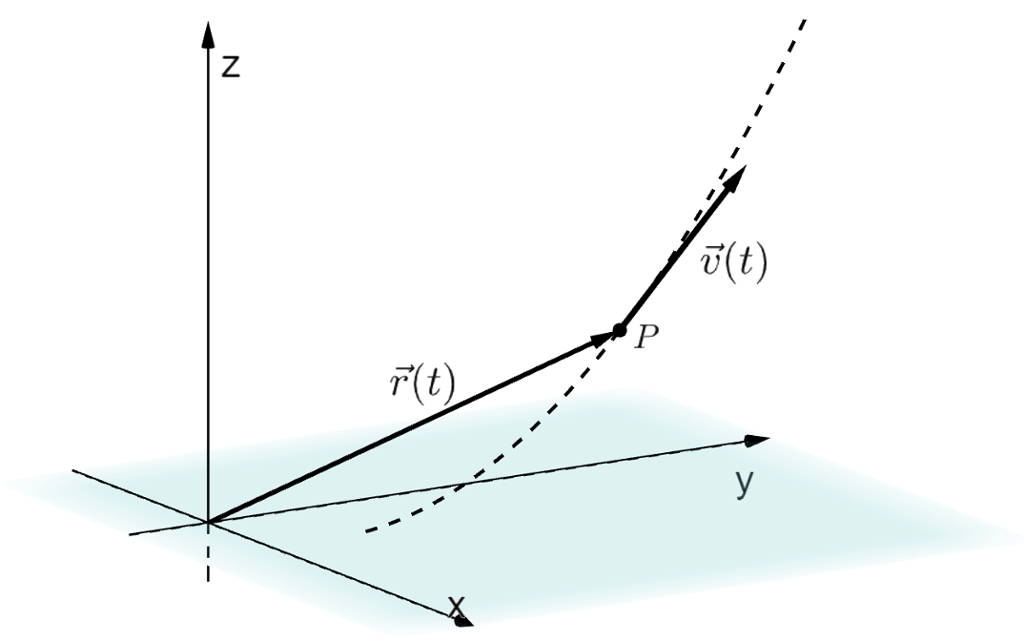
Figuren viser banen til ein rakett som blir skoten opp. Raketten følger ein bane gitt ved kurva $k$.

$k:\left\{\begin{array}{l}x=t+2\\ y=2t+2\\ z=t^2+t\end{array}\right. , t\ge 0$

$t$ er tida målt i sekund etter oppskytingstidspunktet. Vi kan tenke oss at vi måler $x, y$ og $z$ i meter. Vi føreset at $xy$-planet er bakkenivå, og at $z$-aksen peiker loddrett oppover.

Tenk over

Kva blir den tilsvarande vektorfunksjonen $\overrightarrow{r}\left(t\right)$ til kurva $k$?

Aktuelle spørsmål å stille om raketten og banen han følger, er:

1. Kvar blir raketten skoten opp frå?

2. Kor langt har raketten komme etter 2 sekund?

3. Kor høgt har raketten komme etter 2 sekund?

4. Kor fort går raketten då?

5. Kor stor er akselerasjonen til raketten då?

Vi svarer på det første spørsmålet. Oppskytingstidspunktet er $t=0$. Då har raketten posisjonen

$\overrightarrow{r}\left(0\right)=\left[0+2,2·0+2,0^2+0\right]=\left[2,2,0\right]$

Vi finn svaret på det andre spørsmålet ved først å setje $t=2$ inn i vektorfunksjonen. Då får vi at etter 2 sekund har raketten posisjonen

$\overrightarrow{r}\left(2\right)=\left[2+2,2·2+2,2^2+2\right]=\left[4,6,6\right]$

Spørsmålet krev at vi svarer på kor langt raketten har flytta seg. Då må vi rekne ut lengda av vektoren mellom dei to posisjonane.

$\overrightarrow{r}\left(2\right)-\overrightarrow{r}\left(0\right)=\left[4,6,6\right]-\left[2,2,0\right]=\left[2,4,6\right]$

$\left|\left[2,4,6\right]\right|=\sqrt{2^2+4^2+6^2}=\sqrt{4+16+36}=\sqrt{56}$

Høgda til raketten (spørsmål 3) blir det same som $z$-komponenten til $\overrightarrow{r}\left(t\right)$. Vi har då gått ut frå at $xy$-planet er vassrett. Frå utrekninga av $\overrightarrow{r}\left(2\right)$ får vi derfor at raketten er 6 meter over bakken etter 2 sekund.

Dei to siste spørsmåla ventar vi litt med.

Fartsvektoren

På figuren er rakettbanen teikna som ei stipla kurve. $P$ og $Q$ er to punkt i banen. Når raketten flyttar seg frå $P$ til $Q$, endrar posisjonsvektoren seg frå ${\overrightarrow{r}}_1$ til ${\overrightarrow{r}}_2$. Forflyttinga $∆\overrightarrow{r}$ blir derfor ein vektor frå $P$ til $Q$.

Tenk over

Kva blir samanhengen mellom dei tre vektorane ${\overrightarrow{r}}_1$, ${\overrightarrow{r}}_2$ og $∆\overrightarrow{r}$?

Definisjon av fartsvektoren

I fysikkfaget definerer vi gjennomsnittsfarten ${\overrightarrow{v}}_g$ ved ei forflytting $∆\overrightarrow{r}$ som $∆\overrightarrow{r}$ delt på endringa i tid $∆t$, det vil seie den tida det tek å flytte seg frå $P$ til $Q$. Vi får

${\overrightarrow{v}}_g=\frac{∆\overrightarrow{r}}{∆t}$

Legg merke til at vi ikkje definerer gjennomsnittsfarten som banelengda, det vil seie lengda av kurva i det aktuelle tidsrommet, delt på endringa i tid. Sidan likninga er ei vektorlikning, må vektoren ${\overrightarrow{v}}_g$ for gjennomsnittsfart vere parallell med $∆\overrightarrow{r}$.

Vi ønsker å komme fram til den momentane fartsvektoren $\overrightarrow{v}\left(t\right)$ i punktet $P$. Då kan vi sjå for oss at vi flyttar punktet $Q$ nærare og nærare punktet $P$. Jo nærare punktet $P$ punktet $Q$ er, jo betre tilnærming får vi til momentanfarten. Det betyr at

$\overrightarrow{v}\left(t\right)=\underset{∆t\to 0}{\lim }\frac{∆\overrightarrow{r}\left(t\right)}{∆t}$

Dette er definisjonen av den momentane fartsvektoren. Betraktninga er ganske lik det vi gjer i matematikk 1T der vi kjem fram til momentan vekstfart og den deriverte av ein funksjon. Forskjellen er at vi no har ein vektor med tre komponentar, ikkje ein enkelt funksjon. Å ta denne grenseverdien betyr at vi skal la $∆t\to 0$ i kvar av vektorkomponentane. Det betyr vidare at for å finne fartsvektoren, skal vi derivere kvar av vektorkomponentane med omsyn på $t$.

Dersom $\overrightarrow{r}\left(t\right)=\left[x\left(t\right),y\left(t\right),z\left(t\right)\right]$, får vi derfor at

$\overrightarrow{v}\left(t\right)=\left[x^{\text{'}}\left(t\right),y^{\text{'}}\left(t\right),z^{\text{'}}\left(t\right)\right]$

Tenk over

Kva kan vi seie om retninga på $\overrightarrow{v}$ i punktet $P$?

Banefart

Tenk over

Kor fort går eigentleg raketten?

Spørsmål 4 frå dømet

No kan vi svare på spørsmål 4 i rakettdømet over. Når vi spør "Kor fort går raketten etter 2 sekund?", meiner vi "Kor stor er banefarten når $t=2$?".

Først må vi finne den momentane fartsvektoren. Sidan $\overrightarrow{r}\left(t\right)=\left[t+2,2t+2,t^2+t\right]$, får vi

$\begin{array}{rcl}\overrightarrow{v}\left(t\right) & =& \left[x^{\text{'}}\left(t\right),y^{\text{'}}\left(t\right),z^{\text{'}}\left(t\right)\right]=\left[1,2,2t+1\right]\\ \overrightarrow{v}\left(2\right) & =& \left[1,2,2·2+1\right]=\left[1,2,5\right]\\ \left|\overrightarrow{v}\left(2\right)\right| & =& \sqrt{1^2+2^2+5^2}=\sqrt{1+4+25}=\sqrt{30}\end{array}$

Raketten har farten $\sqrt{30} \mathrm{m}/\mathrm{s}\approx 5,5 \mathrm{m}/\mathrm{s}$ etter 2 sekund.

Tenk over

Kvifor blir måleininga for farten i dømet $\mathrm{m}/\mathrm{s}$?

Oppsummering: fart

Vi har ein partikkel med posisjon gitt ved ein vektorfunksjon

$\overrightarrow{r}\left(t\right)=\left[x\left(t\right),y\left(t\right),z\left(t\right)\right]$

der parameteren $t$ står for tida. Då er den momentane fartsvektoren $\overrightarrow{v}\left(t\right)$ bestemd ved

$\overrightarrow{v}\left(t\right)=\underset{∆t\to 0}{\lim }\frac{∆\overrightarrow{r}\left(t\right)}{∆t}=\left[x^{\text{'}}\left(t\right),y^{\text{'}}\left(t\right),z^{\text{'}}\left(t\right)\right]$

Vi skriv òg ofte

$\overrightarrow{v}\left(t\right)={\overrightarrow{r}}^{ \text{'}}\left(t\right)$

$\overrightarrow{v}\left(t\right)$ er i alle punkt parallell med tangenten til rørslekurva i punktet.

Banefarten er lengda av fartsvektoren, det vil seie$\left|\overrightarrow{v}\left(t\right)\right|$. Banefarten er den farten vi kan måle at partikkelen har uavhengig av retning.

Akselerasjonsvektoren

Akselerasjon er eit mål på kor raskt farten endrar seg. Vi kan gjere tilsvarande betraktning av fartsendringa som vi gjorde med posisjonsendringa over. Derfor er den momentane akselerasjonsvektoren i fysikken definert som

$\overrightarrow{a}\left(t\right)=\underset{∆t\to 0}{\lim }\frac{∆\overrightarrow{v}\left(t\right)}{∆t}$

Dette gir oss vidare at

$\overrightarrow{a}\left(t\right)={\overrightarrow{v}}^{ \text{'}}\left(t\right)={\left({\overrightarrow{r}}^{ \text{'}}\left(t\right)\right)}^{\text{'}}={\overrightarrow{r}}^{ \text{'}\text{'}}\left(t\right)=\left[x^{\text{'}\text{'}}\left(t\right),y^{\text{'}\text{'}}\left(t\right),z^{\text{'}\text{'}}\left(t\right)\right]$

Akselerasjonsvektoren er den deriverte av fartsvektoren og dermed den andrederiverte av posisjonsvektoren.

Når det i ei oppgåve blir spurt etter akselerasjonen, er det vanlegvis absoluttverdien av akselerasjonsvektoren, $\left|\overrightarrow{a}\left(t\right)\right|$, som er meint. I nokre tilfelle kan det òg spørjast etter retninga på akselerasjonsvektoren.

Spørsmål 5 frå dømet

No kan vi svare på spørsmål 5 i rakettdømet over. Når vi spør "Kor stor er akselerasjonen til raketten etter 2 sekund?", meiner vi "Kor stor er $\left|\overrightarrow{a}\left(2\right)\right|$?".

Først må vi finne akselerasjonsvektoren. Sidan $\overrightarrow{v}\left(t\right)=\left[1,2,2t+1\right]$, får vi

$\overrightarrow{a}\left(t\right)={\overrightarrow{v}}^{ \text{'}}\left(t\right)=\left[0,0,2\right]$

Det betyr at akselerasjonen er konstant sidan han ikkje varierer med $t$. Sidan $x$- og $y$-komponentane er null, er akselerasjonen loddrett og lik $2 \mathrm{m}/{\mathrm{s}}^2$ etter 2 sekund og til alle andre tidspunkt.

Tenk over

Kvifor blir måleininga for akselerasjonen i dømet $\mathrm{m}/{\mathrm{s}}^2$?