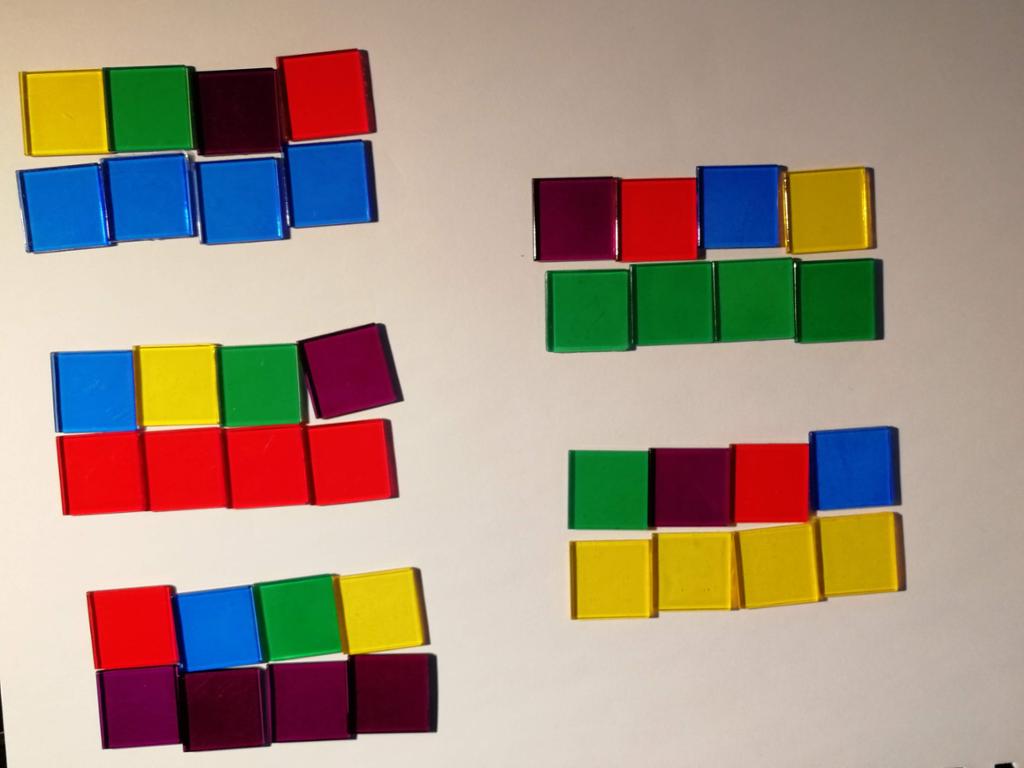Introduksjon til kombinatorikk

Kombinatorikk er ei grein innan matematikk vi kan bruke til å finne ut på kor mange ulike måtar vi kan kombinere element etter ulike kriterium. Enkelt sagt er kombinatorikk oppteljing av kor mange ulike utfall vi kan få i eit forsøk.

Som ein introduksjon til kombinatorikk ønskjer vi å gjere ei lita øving. Dersom skulen din har teljebrikker i ulike fargar, kan dei vere ei god hjelp. Dersom ikkje du har slike brikker for handa, kan du teikne med ulike fargar eller skrive ulike symbol.

For å gjere denne øvinga treng du brikker i fem ulike fargar. Du bør ha omtrent 10–15 av kvar farge.

No skal du prøve å finne ut kor mange ulike par du kan lage med to av desse fem fargane. Slå deg gjerne saman med ein medelev, og prøv dykk fram. Er de samde om kva kriterium de skal bruke? Får de ulike svar? Er nokon av desse svara meir rett enn dei andre?

Vent gjerne ei stund med å opne tipsboksen under – her finn du noko å tenkje nærare gjennom.

Løysing nummer 1

Først ser vi på korleis vi kan få 25 til svar. På biletet under har vi laga fem grupper der vi har fem ulike par i kvar gruppe, det vil seie at vi har 25 par. Vi ser at vi har med par der dei to brikkene har lik farge, og vi har òg med kombinasjonen av til dømes blå og grøn to gonger. Dette er éin måte å lage par med to brikker på når vi har brikker med fem ulike fargar å velje mellom.

Vi kan observere at vi kunne ha funne det ut ved rekning ved å tenkje at vi har fem moglegheiter for første brikke, og for kvar av desse moglegheitene har vi fem moglegheiter, altså $$ 5·5$$ moglegheiter.

Løysing nummer 2

I løysing nummer 1 såg vi at vi hadde med løysingar der dei to brikkene var like. Vi kan jo tenkje oss ein situasjon der det ikkje er mogleg å ha to like, til dømes dersom vi berre har ei av kvar brikke. Dersom vi no tek vekk alle dei para med to like brikker, sit vi igjen med fem grupper med fire par i kvar gruppe, altså $$ 5·4=20$$ par.

Utan å bruke brikkene og lage figurane kunne vi ha tenkt som i løysing nummer 1: Vi har fem moglegheiter for brikke nummer 1, men no berre fire moglegheiter for brikke nummer 2.

Løysing nummer 3

Dersom vi kikkar nøye på løysing nummer 2, ser vi at alle fargekombinasjonane finst to gonger. Nokre gonger kan rekkjefølgja på teljebrikkene ha noko å seie. Vi kan til dømes lage eit kodespråk der raud-blå betyr noko anna enn blå-raud. Vi kan òg tenkje oss situasjonar der det ikkje har noko å seie kva rekkjefølgje vi legg teljebrikkene i, og at det einaste som betyr noko, er om vi har til dømes ei raud og ei blå eller ei gul og ei grøn brikke. I det siste tilfellet kan vi fjerne halvparten av para, og vi sit igjen med $$ \frac{5·4}{2}=10$$ par som på biletet under.

Løysing nummer 4

Vi kan òg tenkje oss at vi ønskjer oss berre par der ingen av para kan forvekslast med kvarandre (altså vil vi ikkje ha med til dømes både raud-blå og blå-raud), men vi kan gjerne ha med dei para der begge brikkene er like. Då kan vi leggje desse para tilbake igjen, og vi får 15 par som på biletet under.

Vi sa innleiingsvis at kombinatorikk handlar om å telje opp talet på utfall i eit forsøk. Vi kan sjå på øvinga med teljebrikkene som eit forsøk med fem teljebrikker i fem ulike fargar i ein hatt. Vi trekkjer to teljebrikker frå hatten på den måten at vi trekkjer éi og éi brikke.

Talet på ulike utfall vi får i forsøket, avheng av to ting:

• Legg vi tilbake den første brikka før vi trekkjer brikke nummer to? Dersom vi gjer det, er to like brikker eit mogleg utfall. Utan tilbakelegging har vi ikkje denne moglegheita.
• Skal vi oppfatte til dømes blå brikke i første trekk og raud brikke i andre trekk som det same utfallet som raud brikke i første trekk og blå brikke i andre trekk? Sagt på ein enklare måte: Skal rekkjefølgja bety noko? Dersom rekkjefølgja betyr noko, har vi eit ordna utval, elles er det eit uordna utval.

I løysing nummer 1 har vi ordna utval med tilbakelegging. Vi får eit utval med 25 ulike utfall.

I løysing nummer 2 har vi ordna utval utan tilbakelegging. Vi får eit utval med 20 ulike utfall. Dei fem moglege utfalla med like brikker forsvinn.

I løysing nummer 3 har vi uordna utval utan tilbakelegging. Vi halverer talet på utfall i forhold til løysing nummer 2, sidan rekkjefølgja ikkje betyr noko, og vi endar på 10 utfall. Raud pluss blå er same utfall som blå pluss raud.

I løysing nummer 4 har vi uordna utval med tilbakelegging. Vi tek med dei fem utfalla med like brikker igjen, og vi får fem fleire utfall enn i løysing nummer 3.

Dei tre første typane av utval skal du få bli godt kjend med i artikkelen "Tre ulike typar utval", men før vi kjem så langt, skal vi jobbe litt med fakultet og binomialformelen.