Introduksjon til andregradsfunksjonar som modellar
I lineære funksjonar opptrer variabelen berre i første potens. Ein andregradsfunksjon har i tillegg eit ledd der variabelen opptrer i andre potens. Det vil seie at vi har ledd som inneheld . Ein andregradsfunksjon har ikkje ledd med høgare potens av enn 2.
Gå saman med nokre medelevar og bruk eit tau som er litt over 12 meter langt. Bind saman endane og form tauet til eit rektangel som figuren viser. Omkrinsen til rektangelet skal vere 12 meter.
I eit rektangel er to og to sider er like lange, slik at vi berre har to forskjellige sidelengder. Vi kallar desse for høvesvis grunnlinje og høgde her.
La først grunnlinja vere 1 meter. Lag eit rektangel av tauet og mål lengda av høgda. Rekn ut arealet av rektangelet.
Lag ein verditabell der de noterer resultata av målingane og utrekninga.
Gjer så det same fleire gonger, men varier lengda på grunnlinja til høvesvis 2 meter, 3 meter, 4 meter, 5 meter og til slutt 6 meter.
Før alle resultata inn i same verditabell.
Plott så resultata i eit koordinatsystem der de på -aksen avset lengda av grunnlinja og på -aksen avset areala. Skisser ei kurve gjennom punkta.
Kor lang må grunnlinja vere for å få størst areal?
La no grunnlinja vere meter.
- Kan de finne ein formel for høgda?
- Kan de så finne ein formel for arealet som funksjon av grunnlinja, ?
- Bruk GeoGebra og teikn grafen som viser arealet som funksjon av grunnlinja, .
- Plott inn punkta frå verditabellen i same koordinatsystem. Kva ser de?
- Samanlikn denne grafen med den grafen de skisserte. Kva finn dere?
- Kva er det maksimale arealet firkanten kan få?
- Kva fortel grafen sine skjeringspunkt med -aksen?
Løysing
For kvar verdi av får vi eit bestemt rektangel med eit bestemt areal. Vi har altså at arealet til rektangelet er ein funksjon av . Omkrinsen til rektangelet er 12 meter. To og to sider er like lange, slik at vi berre har to forskjellige sidelengder. Vi kallar desse for høvesvis grunnlinje og høgd. Grunnlinja og høgda må til saman vere halve omkrinsen, slik at når grunnlinja er , så må høgda vere .
Formelen, modellen, for arealet som funksjon av grunnlinja blir då
Vi har ein andregradsfunksjon.
Her er funksjonen representert ved ein verditabell:
Grunnlinja i meter | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
Høgda i meter | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Areal av rektangel i m2 | 0 | 5 | 8 | 9 | 8 | 5 | 0 |
I nedste linje har vi rekna ut arealet av rektangelet for dei forskjellige verdiane av .
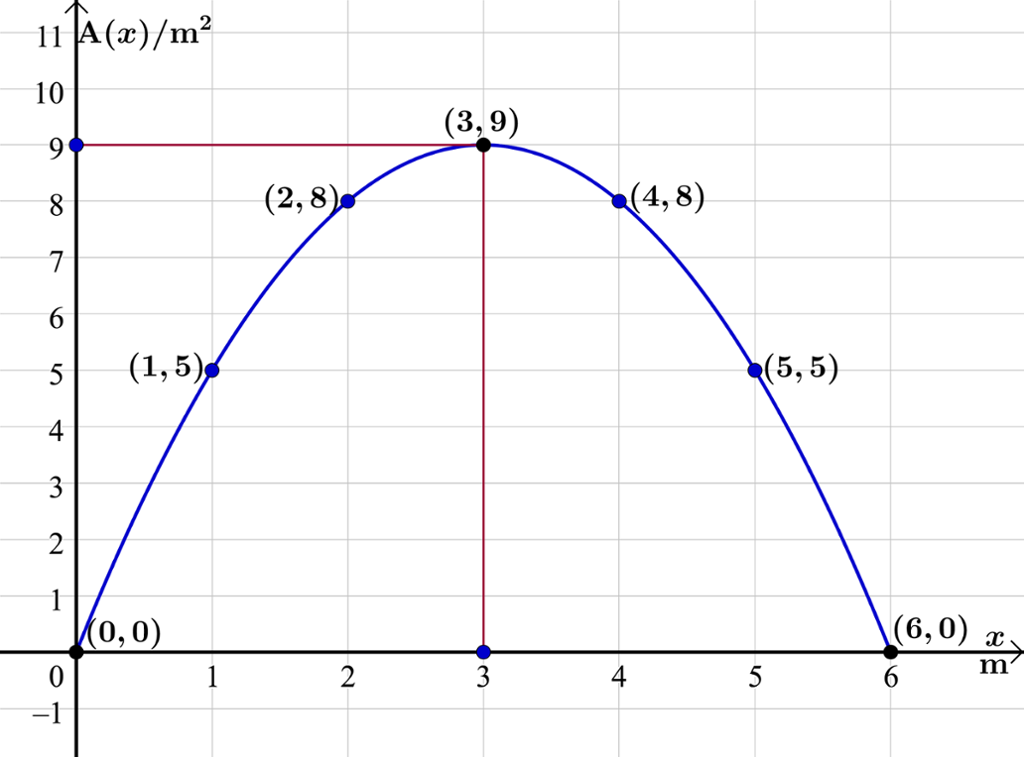
Vi har plotta punkta frå verditabellen i eit koordinatsystem der førstekoordinaten er lengda på grunnlinja og andrekoordinaten er arealet til det tilhøyrande rektangelet.
Vi teiknar grafen til funksjonen i same koordinatsystem og ser at grafen går gjennom punkta som vi plotta frå verditabellen.
Grafen har eit toppunkt, eit punkt der funksjonen har sin maksimale verdi. Det vil seie at det største arealet rektangelet kan få, er .
Nullpunkta finn vi der grafen skjer førsteaksen, altså anten ved 0 eller 6 meter. Vi får då ikkje noko reelt rektangel, og arealet blir 0.

Preikestolen er eit fjellplatå i Rogaland som ragar ca. 600 meter over Lysefjorden. Fjellveggen frå Preikestolen ned til fjorden er nesten loddrett.
Tenk deg at du står på kanten av Preikestolen og kastar ein stein rett opp i lufta med utgangsfart . På nedturen passerer steinen på utsida av platået og hamnar i Lysefjorden.
Naturlovene fortel oss at høgda til steinen er ein funksjon av tida og er tilnærma gitt med funksjonsuttrykket
Her står for tida i sekund etter at steinen vart kasta.
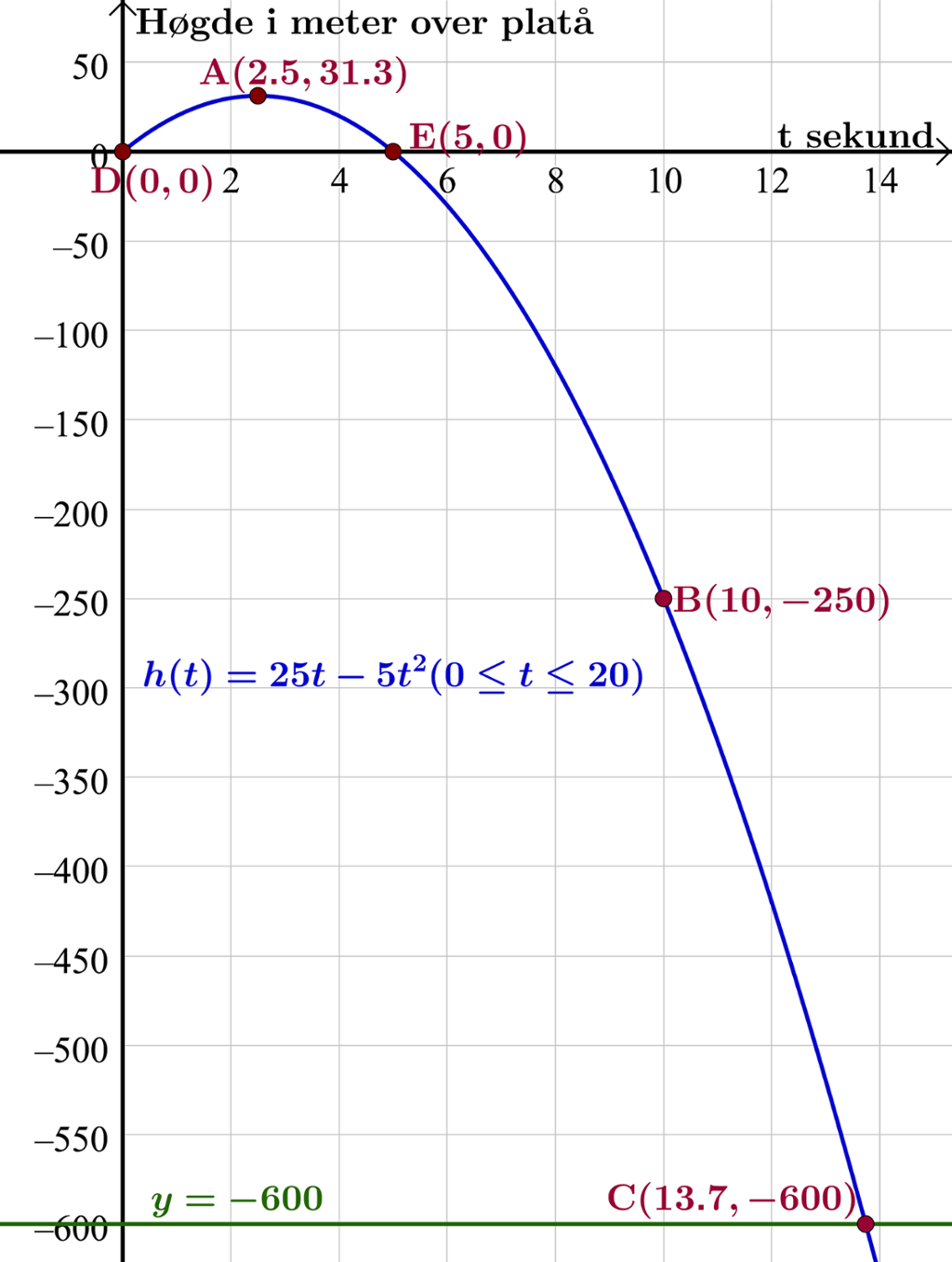
Høgdefunksjonen er ein andregradsfunksjon fordi variabelen er i andre potens.
Vi teiknar grafen til funksjonen dei første 20 sekunda ved å skrive h(t)=Funksjon[25t-5t^2, 0, 20].
Vi finn toppunktet til dømes ved kommandoen Ekstremalpunkt[h]. Det viser at steinen når det høgaste punktet sitt 31,3 meter over platået etter 2,5 sekund.
Vi finn punktet ved å skrive (10,h(10)). Det viser at steinen passerer 250 meter under platået etter 10 sekund.
Vi teiknar linja og finn skjeringspunktet mellom denne linja og grafen til dømes ved kommandoen Skjering mellom to objekt. Vi får skjeringspunktet , som viser at steinen treffer Lysefjorden etter 13,7 sekund.
Vi finn nullpunkta og til dømes ved kommandoen Nullpunkt[h]. Det viser at steinen forlèt platået ved tida null og passerer platået på vegen ned etter 5 sekund.