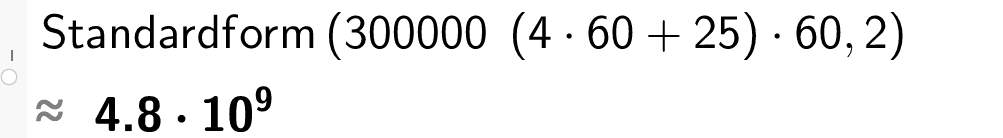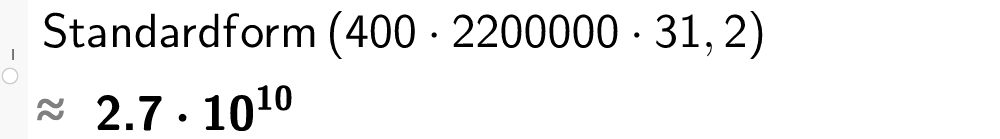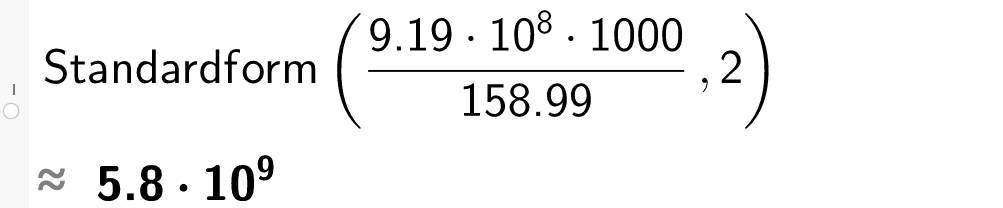Skriv desse tala som tiarpotensar.
a) 1 000 000
Løysing 1 000 000 = 10 6
b) 0 , 1
Løysing 0 , 1 = 10 - 1
c) 0 , 000 000 001
Løysing 0 , 000 000 001 = 10 - 9
d) 1 000
Løysing 1 000 = 10 3
Skriv tiarpotensane om til tal.
a) 10 2
Løysing 10 2 = 100
b) 10 5
Løysing 10 5 = 100 000
c) 10 - 3
Løysing 10 - 3 = 0 , 001
d) 10 - 7
Løysing 10 - 7 = 0 , 000 000 1
Skriv desse tala på standardform
a) 2 000 000
Løysing 2 000 000 = 2 · 10 6
b) 1 200 000
Løysing 1 200 000 = 1 , 2 · 10 6
c) 34 000
Løysing 34 000 = 3 , 4 · 10 4
d) 123 400 000
Løysing 123 400 000 = 1 , 234 · 10 8
Skriv desse tala på standardform
a) 0 , 002
Løysing 0 , 002 = 2 · 10 - 3
b) 0 , 000 023
Løysing 0 , 000 023 = 2 , 3 · 10 - 5
c) 0 , 046
Løysing 0 , 046 = 4 , 6 · 10 - 2
d) 0 , 000 000 678
Løysing 0 , 000 000 678 = 6 , 78 · 10 - 7
Rekn ut og skriv svaret på standardform.
a) 2 , 5 · 10 5 · 6 , 0 · 10 3
Løysing 2 , 5 · 10 5 · 6 , 0 · 10 3 = 2 , 5 · 6 , 0 · 10 5 + 3 = 15 , 0 · 10 8 = 1 , 5 · 10 9
b) 9 , 2 · 10 5 · 2 000
Løysing 9 , 2 · 10 5 · 2 000 = 9 , 2 · 10 5 · 2 · 10 3 = 9 , 2 · 2 · 10 3 + 5 = 18 , 4 · 10 8 = 1 , 84 · 10 9
c) 7 , 5 · 10 - 5 · 2 , 0 · 10 - 3
Løysing 7 , 5 · 10 - 5 · 2 , 0 · 10 - 3 = 15 · 10 - 5 - 3 = 1 , 5 · 10 - 7
d) 25 · 10 5 0 , 5 · 10 - 3
Løysing 25 · 10 5 0 , 5 · 10 - 3 = 25 · 10 5 5 · 10 - 4 = 5 · 10 5 - ( - 4 ) = 5 · 10 9
e) 2 , 5 · 10 5 · 6 , 0 · 10 3 0 , 5 · 10 7
Løysing 2 , 5 · 10 5 · 6 , 0 · 10 3 0 , 5 · 10 7 = 2 , 5 5 · 10 5 · 6 , 0 · 10 3 0 , 5 · 10 7 = 30 · 10 5 + 3 - 7 = 3 , 0 · 10 2
f) 5 · 10 - 5 · 1 , 2 · 10 3 6 · 10 - 3
Løysing 5 · 10 - 5 · 1 , 2 · 10 3 6 · 10 - 3 = 6 · 10 - 5 + 3 6 · 10 - 3 = 1 · 10 - 2 - - 3 = 1 · 10 1
g) 5 000 · 0 , 000 6 250 000
Løysing 5 000 · 0 , 000 6 250 000 = 5 2 · 10 3 · 6 · 10 - 4 2 , 5 · 10 5 = 12 · 10 3 - 4 - 5 = 12 · 10 - 6 = 1 , 2 · 10 - 5
h) 25 · 10 5 · 0 , 000 7 7 · 10 - 3 · 2 5000
Løysing 25 · 10 5 · 0 , 000 7 7 · 10 - 3 · 2 5000 = 25 · 10 5 · 7 · 10 - 4 7 · 10 - 3 · 25 · 10 3 = 25 · 7 7 · 25 · 10 5 - 4 - - 3 - 3 = 1 · 10 1
Løys denne oppgåva i GeoGebra.
Når vi snakkar om avstandar i universet, bruker vi ofte nemninga lysår. Eit lysår er den avstanden lyset beveger seg i løpet av eitt år. Lyset har ein fart på 300 000 km/s.
a) Kor mange kilometer er eit lysår?
Løysing Eit lysår er 9 , 5 · 10 12
Lyset bruker 4 timar og 25 minutt mellom jorda og dvergplaneten Pluto.
b) Kva er avstanden mellom jorda og Pluto?
Løysing Avstanden mellom jorda og Pluto er · ( 4 · 60 + 25 ) · 60 s ≈ 4 , 8 · 10 9
Løys oppgåva i GeoGebra.
I oktober 2008 produserte Noreg 2,2 millionar fat råolje dagleg. Vi reknar med ein pris på råolje på 400 kroner per fat.
a) Kor mange milliardar kroner var verdien av oljeproduksjonen på denne månaden?
Løysing Verdien av oljeproduksjonen var
400 kroner/fat· 2 , 2 · 10 6 · 31 ≈ 2 , 7 · 10 10 27 · 10 9
I internasjonal oljeomsetning svarer eit fat til 42 amerikanske gallon eller 158,987 liter.
b) Kor mange liter råolje produserte Noreg denne månaden? Gi svaret på standardform.
Løysing Produksjonen var på· 2 , 2 · 10 6 · 31 ≈ 1 , 1 · 10 10
Det vart hevda at råoljereservane på norsk sokkel i 2008 var på 919 millionar kubikkmeter råolje.
c) Kor mange fat olje svarer dette til?
Løysing Det svarer til 5 , 8 · 10 9
Rekn med den same oljeproduksjonen som i oktober 2008.
d) Kor lenge vil oljereservane vare med ei slik utrekning?
Løysing Oljereservane vil vare i
9 , 19 · 10 11 L 1 , 084 · 10 10 L / månad · 12 månad / år ≈ 7 , 06 år
Kva kan du om potensar og tal på standardform?
Her kan du laste ned oppgåvene som word- og pdf-dokument.