Drøfting av polynomfunksjoner

Å finne ut hvor grafen til en funksjon stiger og hvor grafen synker, kalles for å drøfte funksjonens monotoniegenskaper.
Å drøfte en funksjon betyr gjerne at vi skal undersøke monotoniegenskapene og bestemme topp- og bunnpunkter på grafen. En fellesbetegnelse for topp- og bunnpunkter er ekstremalpunkter.
Her kommer en utfordring:
Tegn grafen til tredjegradsfunksjonen gitt ved
Tegn deretter tangenter til grafen for noen -verdier mellom og .
Undersøk om det er en sammenheng mellom tangentenes stigningstall og hvorvidt grafen stiger, synker eller har topp- eller bunnpunkter.
Her kan du se at
- stigningstallet til tangenten er positivt når grafen stiger for stigende -verdier
- stigningstallet til tangenten er negativt når grafen synker for stigende -verdier
- stigningstallet til tangenten er null i topp- og bunnpunkter for stigende -verdier
Siden tangentens stigningstall er lik den deriverte til funksjonen, betyr dette følgende:
Når grafen stiger for stigende -verdier, er den deriverte positiv. Det motsatte gjelder også: Hvis den deriverte er positiv, så stiger grafen.
Når grafen synker for stigende -verdier, er den deriverte negativ. Det motsatte gjelder også: Hvis den deriverte er negativ, så synker grafen.
Når grafen har topp- eller bunnpunkt, er den deriverte lik null.
Dette betyr at vi kan finne ut for hvilke verdier av grafen til en funksjon stiger, for hvilke verdier av den synker og når den har topp- eller bunnpunkt ved å se på fortegnet til den deriverte. Vi viser dette gjennom noen eksempler.
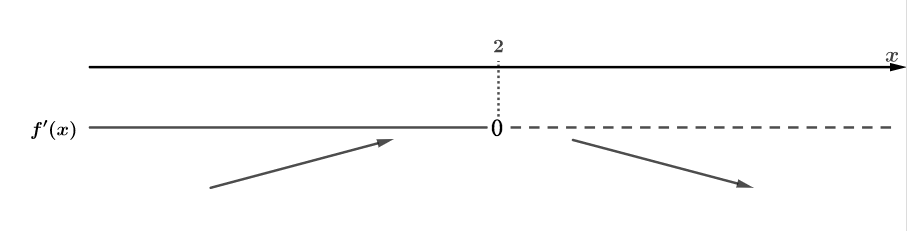
Vi skal finne eventuelle ekstremalpunkter (topp- og bunnpunkter) til en funksjon der den deriverte funksjonen har følgende graf:
Løsning
Den deriverte funksjonen, , har nullpunktene og .
For er positiv, som betyr at grafen til stiger. For er negativ, som betyr at grafen til synker. Det betyr at funksjonen har et toppunkt for .
For
Vi tegner grafen til en funksjon som passer med opplysningene ovenfor:
Drøft monotoniegenskapene til en funksjon der den deriverte funksjonen har grafen under til høyre.
Funksjonen
Lag en skisse av grafen til
Løsning
Vi kan sette opp fortegnslinja til
Vi legger merke til at den deriverte ikke skifter fortegn i nullpunktet. Den deriverte er positiv for
Nedenfor har vi tegnet en skisse av grafen til
Definisjon
Gitt funksjonen
Et stasjonært punkt er et toppunkt eller et bunnpunkt hvis
Et terrassepunkt er et stasjonært punkt hvor funksjonen ikke endrer seg fra voksende til avtagende eller fra avtagende til voksende. Det vil si at den deriverte ikke skifter fortegn.
Stasjonære punkter kan være topp- eller bunnpunkter eller terrassepunkter.
På grunnlag av den deriverte funksjonen
Løsning
Vi setter
Det er bare i nullpunktene at uttrykket for den deriverte kan skifte fortegn. Vi velger derfor tilfeldige
Vi kan da sette opp fortegnslinja til
Vi ser av fortegnslinja at grafen vokser for
Grafen til
Vi vet at hvis toppunktet ligger over
En mulig funksjon er derfor
Toppunktet for denne funksjonen er
Vi tegner grafen i GeoGebra og ser at det vi har funnet ut uten hjelpemidler er riktig.
Vi skal drøfte monotoniegenskapene til
I tillegg skal vi finne nok opplysninger om funksjonen til å tegne en skisse av grafen.
Løsning
Vi deriverer funksjonen.
Vi setter
Det er bare i nullpunktene at uttrykket for den deriverte kan skifte fortegn. Vi velger derfor tilfeldige verdier i hvert av de aktuelle intervallene
Vi kan da sette opp fortegnslinja til
Vi ser av fortegnslinja at
- Grafen synker for
x ∈ ⟨ ← , - 2 ⟩ x ∈ ⟨ 1 3 , → ⟩ - Grafen stiger for
x ∈ ⟨ - 2 , 1 3 ⟩
Grafen til
Toppunktet er
Bunnpunktet er
Det gjenstår nå å finne nullpunktene til
Funksjonsuttrykket til
Vi prøver om
Det betyr
Vi foretar polynomdivisjonen:
Nå er
Vi løser så likningen
Det betyr at
På grunnlag av de opplysningene vi nå har, kan vi tegne en skisse av grafen. Vi tegner her grafen i GeoGebra:
En liten ting til
Dersom en funksjon er avgrenset på et lukket intervall, som for eksempel