Gjennomsnittlig og momentan vekstfart

Eksempel på gjennomsnittlig vekstfart: kroppshøyde

Som 13-åring var Nils Henrik 149 cm høy. Da han var 17, var han 181 cm. Hvor mye vokste Nils Henrik i denne perioden i gjennomsnitt per år?

Tenk over

Kan vi finne ut hvor høy Nils Henrik var da han var 14 år?

Forklaring

Vi kan ikke ut ifra disse opplysningene vite nøyaktig hvor høy Nils Henrik var da han var 14 år. Men vi kan bruke den gjennomsnittlige vekstfarten til å regne ut hvor høy han tilnærmet var.

Siden han i gjennomsnitt vokste 8 cm per år, ville høyden hans da han var 14 år, være tilnærmet 157 cm.

$$ 149 \mathrm{cm}+8 \mathrm{cm}=157 \mathrm{cm}$$

Hva har vi brukt som forutsetning i utregningen i boksen over?

Forutsetning

Vi har antatt at Nils Henrik vokste like mye hvert år, altså 8 cm per år. Slik var det sikkert ikke i virkeligheten, for ofte vokser barn og ungdom mye det ene året, mens det neste året vokser de nesten ingenting.

I eksempelet over er størrelsen $$ y$$ høyden til Nils Henrik målt i cm og $$ x$$ er tida målt i år. Hva blir den gjennomsnittlige vekstfarten til Nils Henrik dersom vi måler høyden $$ y$$ i mm og bruker måned som enhet på $$ x$$?

Gjennomsnittlig vekst per måned

$$ \frac{320 \mathrm{mm}}{4·12 \mathrm{mnd}}=6,7\frac{\mathrm{mm}}{\mathrm{mnd}}$$

Gjennomsnittlig vokste Nils Henrik 6,7 mm per måned. Dette er den gjennomsnittlige vekstfarten til Nils Henrik når vi måler i millimeter per måned.

Gjennomsnittlig vekstfart grafisk

Vi skal nå se hvordan gjennomsnittlig vekstfart ser ut grafisk.

Tegn informasjonen om alderen til Nils Henrik som to punkter i et koordinatsystem der vi har alderen målt i år på $$ x$$-aksen og høyden målt i cm på $$ y$$-aksen.

Høydeutviklingen til Nils Henrik

Øverst på siden regnet vi ut den gjennomsnittlige vekstfarten med regnestykket

$$ \frac{181 \mathrm{cm}-149 \mathrm{cm}}{17 \mathrm{år}-13 \mathrm{år}}=\frac{32 \mathrm{cm}}{4 \mathrm{år}}$$

Vi finner også igjen tallene i regnestykket i koordinatsystemet i boksen over. Hvor?

Svar

Vi finner tallene som koordinatene til de to punktene.

Vi tegner ei linje gjennom de to punktene, se figuren. Det vannrette, stiplede linjestykket har lengde $$ ∆x$$ lik forskjellen i $$ x$$-verdi mellom de to punktene. Det betyr at

$$ ∆x=17-13=4$$

Tilsvarende har det loddrette linjestykket lengde $$ ∆y$$ lik forskjellen i $$ y$$-verdi mellom de to punktene. Vi får tilsvarende at

$$ ∆y=181-149=32$$

Det betyr at den gjennomsnittlige vekstfarten kan uttrykkes som $$ \frac{∆y}{∆x}$$.

Tenk over

Studer figuren over. Hvilken betydning har forholdet $$ \frac{∆y}{∆x}$$ i tillegg til å være den gjennomsnittlige vekstfarten til Nils Henrik mellom 13 og 17 år?

Forklaring

Vi ser av figuren at den gjennomsnittlige vekstfarten er det samme som stigningstallet til den rette linja gjennom de to punktene.

På figuren har vi tegnet linja ved hjelp av kommandoen "Linje" eller den tilsvarende verktøyknappen. Så har vi brukt kommandoen (eller verktøyknappen) "Stigning" for å finne at stigningstallet til linja er 8.

Gjennomsnittlig vekstfart mellom to punkt

Den gjennomsnittlige vekstfarten fra et punkt $$ \left(x_1,y_1\right)$$ til et punkt $$ \left(x_2,y_2\right)$$, er det samme som stigningstallet $$ a$$ til den rette linja gjennom punktene.

$$ a=\frac{∆y}{∆x}=\frac{y_2-y_1}{x_2-x_1}$$

Gjennomsnittlig vekstfart til en funksjon

Nå antar vi at høyden $$ h$$ til Nils Henrik kan modelleres med funksjonen

$$ h\left(x\right)=-x^2+38x-176 , D_f=\left[12,18\right]$$

der $$ x$$ er alderen i år. Hvordan finner vi nå hvor fort Nils Henrik vokste i gjennomsnitt fra han var 13 til han var 17?

Gjennomsnittlig vekst til Nils Henrik med CAS

Vi finner $$ y$$-koordinatene til de to punktene ved å regne ut $$ h\left(13\right)$$ og $$ h\left(17\right)$$.

Gjennomsnittlig vekst til Nils Henrik grafisk

Vi tegner funksjonen $$ h$$. Så skriver vi inn punktene $$ \left(13,h\left(13\right)\right)$$ og $$ \left(17,h\left(17\right)\right)$$ i algebrafeltet. Deretter tegner vi den rette linja mellom de to punktene med linjeverktøyet (eller kommandoen "Linje") og finner stigningstallet til linja med verktøyet "Stigning".

Dette er nesten samme figur som lenger opp på siden. Forskjellen er at punktene er regnet ut fra en funksjon, mens lenger opp hadde vi oppgitt punktene direkte.

Gjennomsnittlig vekstfart til en funksjon oppsummert

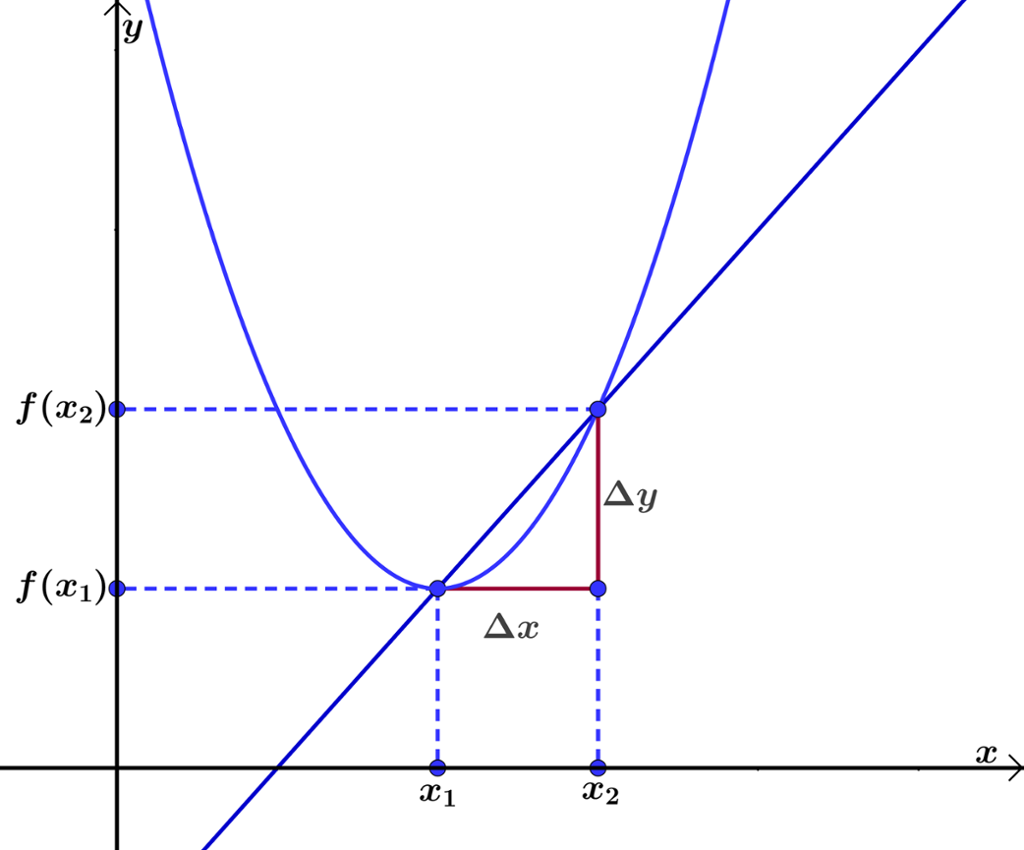
Den gjennomsnittlige vekstfarten for en funksjon $f\left(x\right)$ når $x$ vokser fra $x_1$ til $x_2$, er lik stigningstallet $$ a$$ til sekanten gjennom punktene $\left(x_1, f\left(x_1\right)\right)$ og $\left(x_2, f\left(x_2\right)\right)$.

$a=\frac{\Delta y}{\Delta x}=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$

En sekant er ei rett linje som skjærer en krum kurve i minimum to punkter.

Vi antar fortsatt at høyden til Nils Henrik følger funksjonen

$$ h\left(x\right)=-x^2+38x-176 , D_f=\left[12,18\right]$$

Tenk over

Vi så i eksempelet over at Nils Henrik vokste i gjennomsnitt 8 cm per år fra han var 13 til han var 17. Kan du ut ifra grafen si noe om når i denne perioden han vokste raskest?

Hvor raskt vokste han egentlig per år akkurat da? For å svare på det kan du bruke GeoGebra-simuleringen nedenfor, der du kan dra i den svarte glideren for å flytte på punktet til høyre og observere endringen i stigningstallet til linja. Dersom simuleringen ikke vises, kan du laste den ned nedenfor.

Når vi flytter det svarte punktet til det overlapper det blå, får vi at stigningstallet til linja blir 12. Det betyr at da Nils Henrik var 13 år, vokste han med en fart av 12 cm per år. Merk at dette gjelder bare da han var 13 år, eller når $$ x=13$$. Vi kaller dette for den momentane vekstfarten til Nils Henrik – og til funksjonen $$ h$$ – når $$ x=13$$.

Når de to punktene overlapper, er ikke linja lenger en sekant som skjærer grafen i to punkter, men en tangent til grafen i punktet $$ \left(13,h\left(13\right)\right)$$. Er du enig i at tangenten er like bratt som grafen akkurat i tangeringspunktet? Dette er definisjonen på en tangent.

Momentan vekstfart, definisjon

Den momentane vekstfarten til en funksjon i et punkt på grafen er stigningstallet til tangenten til grafen i dette punktet.

Merk også at både gjennomsnittlig og momentan vekstfart får måleenheten cm/år eller cm per år, altså måleenheten på $$ y$$-aksen delt på måleenheten på $$ x$$-aksen.

Vi kan bruke den momentane vekstfarten til en funksjon som en tilnærming til hvor mye funksjonen vokser når $$ x$$ øker med 1 enhet. I eksempelet her kan vi si at fra Nils Henrik var 13 til han ble 14, vokste han cirka 12 cm siden den momentane vekstfarten til funksjonen når $$ x=13$$, er 12.

Vi skal vise hvordan vi finner den momentane vekstfarten til funksjonen (og Nils Henrik) når $$ x=14$$ både, grafisk og ved regning.

Momentan vekstfart grafisk

Vi har fulgt oppskriften nedenfor da vi lagde bildet i boksen over, bortsett fra at vi tegnet tangenten i punktet $$ \left(13,h\left(13\right)\right)$$, ikke $$ \left(14,h\left(14\right)\right)$$.

• Vi tegner funksjonen ved å skrive den inn i algebrafeltet.

• Vi tegner punktet $$ \left(14,h\left(14\right)\right)$$ ved å skrive nettopp dette i algebrafeltet.

• Vi tegner tangenten til grafen i punktet ved å velge verktøyet "Tangenter", se bildet, klikke på punktet og deretter klikke et sted på grafen til $$ h$$.

• Vi finner stigningstallet til tangenten ved å velge verktøyet "Stigning" og klikke på tangentlinja. Dette stigningstallet er den momentane vekstfarten til grafen i punktet $$ \left(14,h\left(14\right)\right)$$.

Ved å følge disse punktene skal du få at stigningstallet til tangenten er 10. Den momentane vekstfarten til funksjonen når $$ x=14$$, er derfor 10. Det betyr at da Nils Henrik var 14 år, vokste han med 10 cm per år.

Momentan vekstfart med CAS

Vi finner den momentane vekstfarten med CAS enklest på denne måten:

• Skriv inn funksjonen i CAS.

• Vi kombinerer kommandoene "Stigning" og "Tangent" ved å sette tangentkommandoen sammen med den aktuelle $$ x$$-verdien og navnet på funksjonen inn i kommandoen "Stigning". Resultatet blir stigningstallet til tangenten, som er den momentane vekstfarten til funksjonen i tangeringspunktet.

Kommentar: Vi kan også finne tangenten først og deretter bruke kommandoen "Stigning" hvis vi foretrekker å gjøre det på to linjer. Et tredje alternativ er å bare bruke kommandoen "Tangent". Det kan vi gjøre siden vi kan lese ut stigningstallet direkte fra likningen til tangenten.