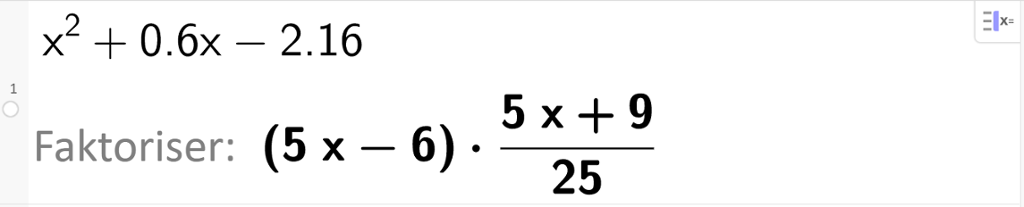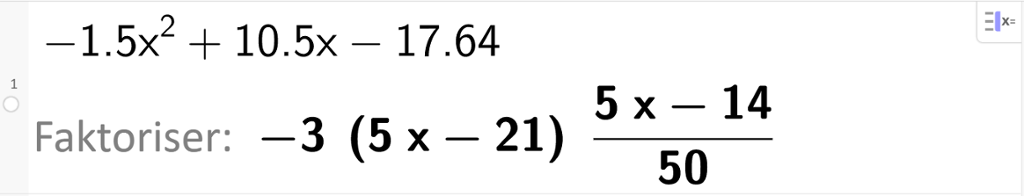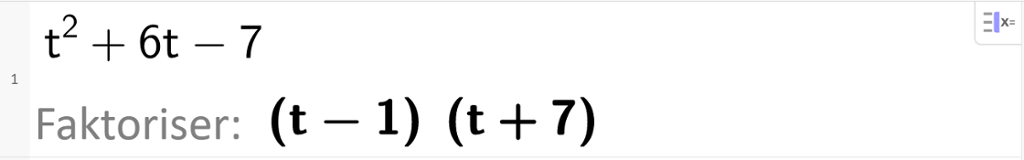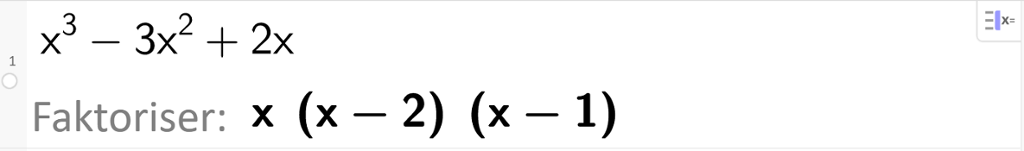Faktoriser utrykkene ved hjelp av nullpunktmetoden.
a)
vis fasit
Vi setter uttrykket lik 0 og får en andregradslikning. Vi løser likningen ved å bruke abc-formelen.
Minner om tegnet "", som betyr "eller".
Da er
b)
vis fasit
Vi setter uttrykket lik 0 og får en andregradslikning. Vi løser likningen ved å bruke abc-formelen.
Da er
c)
vis fasit
Vi setter uttrykket lik 0 og får en andregradslikning. Vi finner løsningene til likningen ved å bruke abc-formelen.
Da er
d)
vis fasit
Vi setter uttrykket lik 0 og får en andregradslikning. Vi finner løsningene til likningen ved å bruke abc-formelen.
Her er det lurt å dividere alle ledd med for å få lettere tall å sette inn i abc-formelen.
Vi får da
Da er
e)
vis fasit
Vi setter uttrykket lik 0 og får en andregradslikning. Vi finner løsningene til likningen ved å bruke abc-formelen.
Her er det lurt å dividere alle ledd med -2 for å få lettere tall å sette inn i abc-formelen.
Vi får da
Da er
Faktoriser uttrykkene
a)
vis fasit
Dette er et fullstendig kvadrat. Bruker andre kvadratsetning.
Dermed er
b)
vis fasit
Vi finner løsningen ved å bruke konjugatsetningen.
c)
vis fasit
Vi finner løsningen ved å bruke konjugatsetningen.
d)
vis fasit
Vi setter uttrykket lik 0 og får en andregradslikning. Vi finner løsningene til likningen ved å bruke abc-formelen.
Likningen har ingen løsning.
Uttrykket kan ikke faktoriseres.
e)
vis fasit
Vi setter uttrykket i parentesen lik 0 og får en andregradslikning. Vi finner løsningene til likningen ved å bruke abc-formelen.
Faktoriseringsformelen gir
Dette betyr videre at
Faktoriser uttrykkene ved hjelp av et digitalt verktøy.
a)
vis fasit
Vi løser oppgaven med CAS i GeoGebra og bruker verktøyknappen Faktoriser eller kommandoen med det samme navnet.
Om vi vil, kan vi skrive svaret slik det er gjort nedenfor.
b)
vis fasit
Vi løser oppgaven med CAS i Geogebra.
Om vi vil, kan vi skrive svaret slik det er gjort nedenfor.
c)
vis fasit
Vi løser oppgaven med CAS i GeoGebra.
Svaret blir .
d)
vis fasit
Vi løser oppgaven med CAS i GeoGebra.
Svaret blir .
e)
vis fasit
Vi løser oppgaven med CAS i GeoGebra.
Svaret blir .