Omdreiningslegemer

Hvis vi dreier grafen til en funksjon 360° om $x$-aksen, vil grafen forme et tredimensjonalt objekt som vi kaller omdreiningslegeme. Formen på et omdreiningslegeme avhenger av formen på grafen, men alle omdreiningslegemer vil ha til felles at de har perfekt symmetri om $$ x$$-aksen.

Hvis grafen for eksempel er ei rett linje, blir omdreiningslegemet ei kjegle eller ei avkortet kjegle. På bildet under har vi lagt inn en rettlinjet graf fra $$ x=1$$ til $$ x=4$$ både i det todimensjonale og det tredimensjonale grafikkfeltet i GeoGebra og en animert framstilling av omdreiningen av dette linjestykket.

Du kan dra i det tredimensjonale grafikkfeltet på figuren over for å se kjegla fra ulike synsvinkler. Du kan også få figuren til å rotere av seg selv ved å dra i grafikkfeltet med musepekeren og så slippe museknappen. Du kan nullstille figuren med knappen med de runde pilene.

En annen mulighet er at grafen har buet form, som for eksempel grafen til $$ f\left(x\right)=\sin x+2, x\in \left[0,7\right]$$. I det interaktive GeoGebra-arket kan du selv teste omdreiningen til denne funksjonen ved å skyve på glidebryteren.

Hva får vi dersom vi dreier ei linje som er parallell med $x$-aksen, $$ 360°$$ om $x$-aksen?

Hvilken form vil omdreiningslegemet få hvis vi dreier en halvsirkel 360° om diameteren?

Vi kan tegne omdreiningslegemer i 3D-grafikkfeltet i GeoGebra, og vi skal vise metoden ved hjelp av funksjonen $$ f\left(x\right)=\frac{1}{x}$$ for $$ x⩾1$$. Omdreining av grafen til denne funksjonen danner et omdreiningslegeme som i matematikk både er kjent som "Gabriels horn" og "Torricellis trompet".

For å få tegnet et omdreiningslegeme i 3D-grafikkfeltet i GeoGebra må vi bruke noen sammenhenger knyttet til parameterframstilling. Dette skal vi se nærmere på i emnet Vektorer og parameterframstillinger i rommet, men "oppskriften" er mulig å bruke allerede nå.

Først må vi vise 3D-grafikkfeltet ved å gå til menyvalget "Vis" i hovedmenyen til GeoGebra. Vi definerer så funksjonen $$ f$$ på vanlig måte i algebrafeltet, og deretter angir vi omdreiningslegemet slik:

Overflate(u,f(u)sin(t),f(u)cos(t),u,1,10,t,0,2pi)

• u representerer i denne sammenhengen den variable i funksjonen, i vårt tilfelle er dette $$ x$$.

• t er variabel for omdreiningen, som angis i radianer.

• f(u)sin(t),f(u)cos(t) representerer koordinatene angitt på parameterform.

• u,1,10 angir definisjonsområdet til u (og dermed til $$ x$$).

• t,0,2pi angir en omdreining fra $$ 0$$ til $$ 2\mathrm{\pi }$$, det vil si en hel omdreining.

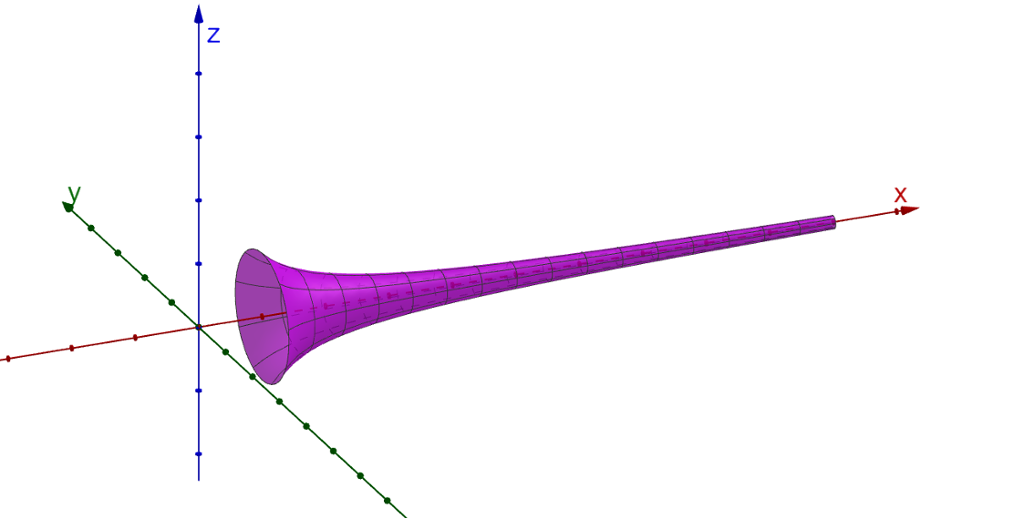
Hvordan kan du lage større "tut" på Gabriels horn, det vil si større diameter på åpningen til venstre på bildet over?

Det er mulig å bruke en forenkling for å tegne omdreiningslegemer i 3D-grafikkfeltet i GeoGebra. Hvis vi skal bruke denne forenklingen, forutsetter vi at funksjonen er angitt med den definisjonsmengden som vi ønsker å gjøre rotasjonen for, og at omdreiningen starter fra $$ t=0$$.

Hvis vi bruker den forenklede formelen for å tegne Gabriels horn, vil vi måtte skrive følgende i algebrafeltet:

Overflate(f,2pi,xAkse)

Som nevnt over må funksjonen $$ f$$ i dette tilfellet være definert slik:

$$ f\left(x\right)=\frac{1}{x}$$, $$ x\in \left[1,10\right]$$

Vi kan også angi rotasjon om de andre to aksene ved å skrive yAkse og zAkse istedenfor xAkse.

Vi kan også lage et omdreiningslegeme ved å dreie et område mellom to grafer. I eksempelet under har vi to funksjoner, $$ f\left(x\right)=2+x^2$$ og $$ g\left(x\right)=4-x^2$$. Det er to skjæringspunkter mellom grafene, for $$ x=-1$$ og $$ x=1$$, og det er området mellom skjæringspunktene som vi dreier om $$ $$$$ x$$-aksen.

For å tegne et omdreiningslegeme som framkommer ved omdreining av et område i 3D-grafikkfeltet i GeoGebra, angir vi overflatene hver for seg.

For å få tegnet omdreiningslegemet som er vist i eksempelet over, vil grenseverdiene være skjæringspunktene, og vi skriver følgende i algebrafeltet i GeoGebra:

Overflate(u,f(u)sin(t),f(u)cos(t),u,-1,1,t,0,2pi)

Overflate(v,g(v)sin(t),g(v)cos(t),v,-1,1,t,0,2pi)

Merk at det må brukes forskjellige variabler (u og v) for funksjonene.

La $f\left(x\right)$ være en vilkårlig funksjon som er definert fra $$ x=x_1$$ til $$ x=x_2$$. Vi tenker at vi dreier flatestykket som avgrenses av grafen til $$ f$$ og $$ x$$-aksen 360° om $x$-aksen. En slik omdreining gir som tidligere nevnt et omdreiningslegeme, som er symmetrisk om rotasjonsaksen.

Hvis vi tenker at vi lager vertikale (loddrette) snitt i et slikt omdreiningslegeme, vil snittflatene være perfekte sirkler, der radius avhenger av hvor i figuren vi lager snittet.

Radius i en slik snittsirkel vil være avstanden fra $$ x$$-aksen til grafen, noe som tilsvarer funksjonsverdien til den aktuelle $x$-verdien.

Vi har da følgende sammenheng: $$ r_{x_i}=f\left(x_i\right)$$.

Arealet av en snittsirkel blir ut fra dette

$$ A\left(x\right)=\pi ·r^2=\pi ·{\left(f\left(x\right)\right)}^2$$

For å kunne beregne volumet av omdreiningslegemet som framkommer ved omdreining av grafen til $$ f$$ mellom $$ x_1$$ og $$ x_2$$, tenker vi oss at vi deler omdreiningslegemet i sylinderformede skiver med tykkelse $∆x$. Volumet av omdreiningslegemet kan da sees på som en sum av volumene av alle disse sylinderformede skivene, som alle har tykkelse $∆x$.

Vi har beregnet volum av romfigurer tidligere, i fagartikkelen "Volum og buelengde", og der kom vi fram til at et uttrykk for det totale volumet er

$$ V={\int }_{x_1}^{x_2}A\left(x\right) dx $$

der $$ A$$ er arealet av flaten av den sylinderformede skiven og $$ dx$$ er høyden av skiven.

Siden vi har funnet at arealet av en sirkelformet skive er $$ A\left(x\right)=\pi ·{\left(f\left(x\right)\right)}^2$$, kan vi utlede en generell formel for volum av omdreiningslegemer:

Hvordan kan vi beregne volum av et omdreiningslegeme som framkommer ved omdreining av et område mellom to grafer?