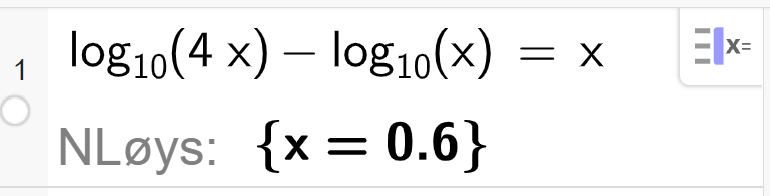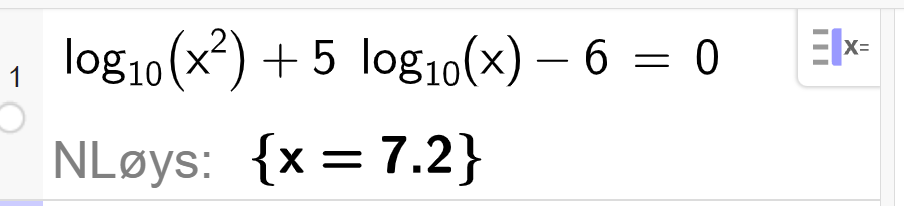Løys likningane ved rekning og med CAS. Hugs parentes når du bruker CAS.
a) lg x = 5
Løysing lg x = 5 x > 0 lg x = 5 x = 10 5 = 100 000
Løyst med CAS:
b) lg 4 x - lg x = x
Løysing lg 4 x - lg x = x lg 4 + lg x - lg x = x x = lg 4 x ≈ 0 , 60
Løyst med CAS:
c) 3 lg x - lg x - 1 = 1
Løysing 3 lg x - lg x - 1 = 1 x > 0 3 lg x - lg x - 1 = 1 2 lg x = 2 lg x = 1 x = 10 1 = 10
Løyst med CAS:
d) lg( x +2) = 4
Løysing lg ( x + 2 ) = 4 x > - 2 lg ( x + 2 ) = 4 x + 2 = 10 4 x = 9998
e) lg x 2 - lg x = 2
Løysing lg x 2 - lg x = 2 x > 0 2 lg x - lg x = 2 lg x = 2 x = 10 2 x = 100
f) lg ( x 2 - 1 ) - lg ( x - 1 ) = 2
Løysing lg ( x 2 - 1 ) - lg ( x - 1 ) = 2 x > 1 lg x 2 + 1 x - 1 = 2 lg ( ( x + 1 ) ( x - 1 ) x - 1 ) = 2 lg ( x + 1 ) = 2 10 lg ( x + 1 ) = 10 2 x + 1 = 100 x = 99
g) lg ( x 2 ) + lg ( x 8 ) = 0
Løysing lg ( x 2 ) + lg ( x 8 ) = 0 lg x - lg 2 + lg x - lg 8 = 0 2 lg x - lg 2 - lg 2 3 = 0 2 lg x - lg 2 - 3 lg 2 = 0 2 lg x = 4 lg 2 lg x = 2 lg 2 lg x = lg 2 2 lg x = lg 4 x = 4
h) lg ( 3 x + 1 ) - lg ( x + 5 ) = 0
Løysing lg ( 3 x + 1 ) - lg ( x + 5 ) = 0 lg ( 3 x + 1 ) = lg ( x + 5 ) 3 x + 1 = x + 5 2 x = 4 x = 2
a) Vi har gitt likninga lg x + 3 = 1
1) For kva verdiar av x
Løysing lg ( x + 3 ) x > - 3
2) Løys likninga ved rekning.
Løysing lg ( x +3) = 1 10 lg ( x + 3 ) = 10 1 x + 3 = 10 x = 7
3) Løys likninga med CAS.
Løysing Løysing med CAS:
b) Vi har gitt likninga 3 · lg ( 2 x - 1 ) = 6
1) For kva verdiar av x
Løysing lg 2 x - 1 er gyldig for x > 1 2 .
2) Løys likninga ved rekning.
Løysing lg ( 2 x - 1 ) = 2 10 lg ( 2 x - 1 ) = 10 2 2 x - 1 = 10 2 x = 100 + 1 2 x = 50 , 5
3) Løys likninga med CAS.
Løysing Løysing med CAS:
c) Vi har gitt likninga (lg x ) 2 + 5 lg x - 6 = 0
1) For kva verdiar av x
Løysing lg x er gyldig for x > 0 .
2) Løys likninga ved rekning.
Løysing lg x = - 5 ± 5 2 - 4 · 1 · ( - 6 ) 2 · 1 lg x = - 5 ± 7 2 lg x = 1 ∨ lg x = - 6 x = 10 ∨ x = 0 , 000 001
3) Løys likninga med CAS.
Løysing Løysing med CAS (merk at vi berre får med éi av løysingane):
d) Vi har gitt likninga lg x 2 + 5 lg x - 6 = 0
1) For kva verdiar av x
Løysing lg x er gyldig for x > 0 .
2) Løys likninga ved rekning.
Løysing 2 lg x + 5 lg x - 6 = 0 7 lg x = 6 lg x = 6 7 x = 10 6 7 ≈ 7 , 2
3) Løys likninga med CAS.
Løysing Løysing med CAS:
e) Vi har gitt likninga lg x 4 - lg x = 18
1) For kva verdiar av x
Løysing lg x er gyldig for x > 0 .
2) Løys likninga ved rekning.
Løysing lg x 4 - lg x = 18 4 lg x - lg x = 18 3 lg x = 18 lg x = 6 10 lg x = 10 6 x = 1 000 000
3) Løys likninga med CAS.
Løysing Løysing med CAS:
f) Vi har gitt likninga ln(4 x - 2) - ln ( 2 x - 2 ) - 2 = 0
1) For kva verdiar av x
Løysing ln 4 x - 2 er gyldig for x > 1 2
ln ( 2 x - 2 ) er gyldig for x > 1
Det betyr at vi berre har løysing når x > 1 .
2) Løys likninga ved rekning.
Løysing ln ( 4 x - 2) - ln ( 2 x - 2 ) - 2 = 0 ln 4 x - 2 2 x - 2 = 2 e ln 2 x - 1 x - 1 = e 2 2 x - 1 x - 1 = e 2 2 x - 1 = e 2 · ( x - 1 ) 2 x - e 2 x = 1 - e 2 x ( 2 - e 2 ) = 1 - e 2 x = 1 - e 2 ( 2 - e 2 ) ≈ 1 , 19
3) Løys likninga med CAS.
Løysing Løysing med CAS:
g) Vi har gitt likninga lg ( x + 2 ) + lg ( x - 1 ) = 1
1) For kva verdiar av x
Løysing lg ( x + 2 ) er gyldig for x > - 2
lg ( x - 1 ) er gyldig for x > 1
Det betyr at vi berre har løysing når x > 1 .
2) Løys likninga ved rekning.
Løysing lg ( x + 2 ) + lg ( x - 1 ) = 1 lg ( x + 2 ) · ( x - 1 ) = 1 10 lg ( x + 2 ) · ( x - 1 ) = 10 1 ( x + 2 ) ( x - 1 ) = 10 x 2 - x + 2 x - 2 = 10 x 2 + x - 12 = 0 ( x - 3 ) ( x + 4 ) = 0 x = 3 ∨ x = - 4
x = - 4
Løysinga er derfor x = 3 .
3) Løys likninga med CAS.
Løysing Løysing med CAS:
h) Vi har gitt likninga ln ( 3 x + 2 ) - ln 2 x = 0
1) For kva verdiar av x
Løysing ln 3 x + 2 er gyldig for x > - 2 3
ln 2 x er gyldig for x > 0
Det betyr at vi berre har løysing når x > 0 .
2) Løys likninga ved rekning.
Løysing ln 3 x + 2 2 x = 0 3 x + 2 2 x = 1 3 x + 2 = 2 x x = - 2
Vi har at x < 0
3) Løys likninga med CAS.
Løysing Løysing med CAS:
Løys likningane.
a) 10 x = 100
Løysing 10 x = 100 lg 10 x = lg 100 x lg 10 = lg 100 x = lg 100 lg 10 x = 2 1 x = 2
b) 10 - 2 x = 100
Løysing 10 - 2 x = 100 - 2 x lg 10 = 2 lg 10 - 2 x = 2 x = - 1
c) 5 x = 125
Løysing 5 x = 125 ln 5 = ln 125 x ln 5 = 3 ln 5 x = 3 ln 5 ln 5 x = 3
d) 2,0 · 0 , 5 x = 16
Løysing 2,0 · 0 , 5 x = 16 lg ( 2,0 · 0 , 5 x ) = lg 16 lg 2 + lg 0 , 5 x = lg 16 lg 2 + x lg 0 , 5 = lg 16 lg 2 + x lg 1 2 = lg 2 4 lg 2 + x ( lg 1 - lg 2 ) = 4 lg 2 x ( lg 1 - lg 2 ) = 4 lg 2 - lg 2 x = 3 lg 2 lg 1 - lg 2 x = 3 lg 2 - lg 2 = - 3
e) 1 4 · 4 2 x = 16
Løysing 1 4 · 4 2 x = 16 4 2 x = 4 2 · 4 4 2 x = 4 3 2 x = 3 x = 3 2
Løys likningane.
a) 4 · 6 x = 36 · 2 x
Løysing 4 · 6 x = 36 · 2 x 6 x = 9 · 2 x ( 2 · 3 ) x = 3 2 · 2 x 2 x · 3 x = 3 2 · 2 x 3 x = 3 2 x = 2
b) 2 2 x + 2 x - 6 = 0
Løysing 2 2 x + 2 x - 6 = 0 2 x 2 + 2 x - 6 = 0
Vi bruker abc-formelen for andregradslikningar.
( 2 x ) 2 + 2 x - 6 = 0 2 x = - 1 ± 1 2 - 4 · 1 · ( - 6 ) 2 · 1 2 x = - 1 ± 25 2 2 x = - 1 + 5 2 ∨ 2 x = - 1 - 5 2 2 x = 2 ∨ 2 x = - 3
2 x = - 3 har inga løysing , sidan 2 x > 0 for alle x .
2 x = 2 x = 1
c) e x - 6 e - x = 1
Løysing e x - 6 e - x = 1 e x · e x - 6 e x · e x = 1 · e x ( e x ) 2 - 6 = e x ( e x ) 2 - e x - 6 = 0 e x = 1 ± ( - 1 ) 2 - 4 · 1 · ( - 6 ) 2 · 1 e x = 1 ± 25 2 e x = 3 ∨ e x = - 2 ( inga løysing for e x mindre enn 0 )
d) 4 2 x - 2 · 4 x - 3 = 0
Løysing 4 2 x - 2 · 4 x - 3 = 0 ( 4 x ) 2 - 2 · 4 x - 3 = 0 4 x = 2 ± ( - 2 ) 2 - 4 · 1 · ( - 3 ) 2 · 1 4 x = 2 ± 4 + 12 2 4 x = 3 ∨ 4 x = - 1 lg 4 x = lg 3 x = lg 3 lg 4
Løys likningane. Hugs at logaritmar berre er definerte for positive tal.
a) lg x = 2 , 24
Løysing lg x = 2 , 24 10 lg x = 10 2 , 24 x = 173 , 78
b) ln x = - 1 , 85
Løysing ln x = - 1 , 85 e ln x = e - 1 , 85 x = 0 , 16
c) 2 · lg x = 0 , 24
Løysing 2 · lg x = 0 , 24 lg x = 0 , 24 2 10 lg x = 10 0 , 12 x = 1 , 32
d) 2 · lg x + 0 , 12 = 0 , 24
Løysing 2 · lg x + 0 , 12 = 0 , 24 lg x + 0 , 06 = 0 , 12 lg x = 0 , 06 10 lg x = 10 0 , 06 x = 1 , 15
e) 2 · ln x - 2 , 0 = 0
Løysing 2 · ln x - 2 , 0 = 0 ln x - 1 = 0 ln x = 1 e ln x = e 1 x = e
f) 2 · lg x 2 - 3 lg x = 0 , 24
Løysing 2 · lg x 2 - 3 lg x = 0 , 24 2 · 2 lg x - 3 lg x = 0 , 24 lg x = 0 , 24 10 lg x = 10 0 , 24 x = 1 , 74
g) lg x 2 - lg 2 x = lg 8
Løysing lg x 2 - lg 2 x = lg 8 2 lg x - ( lg 2 + lg x ) = lg 8 2 lg x - lg 2 - lg x = lg 2 3 lg x = 3 lg 2 + lg 2 = 4 lg 2 = lg 2 4 10 lg x = 10 lg 2 4 x = 16
h) lg x 2 - 2 lg x + lg 4 = 0
Løysing lg x 2 - 2 lg x + lg 4 = 0 lg x - lg 2 - 2 lg x + lg 2 2 = 0 - lg x - lg 2 + 2 lg 2 = 0 - lg x + lg 2 = 0 lg 2 = lg x 10 lg 2 = 10 lg x 2 = x
Vurder løysingsforslaga og diskuter kva elevane har tenkt. Kva logaritmereglar må ein bruke? Klarer du å lage eit betre løysingsforslag? Oppgåva eignar seg fint for diskusjon i små grupper.
Løysing Løysing på oppgåve 1:
7 x = 3 x + 1 lg 7 x = lg 3 x + 1 x lg 7 = ( x + 1 ) lg 3 x lg 7 = x lg 3 + lg 3 x lg 7 - x lg 3 = lg 3 x ( lg 7 - lg 3 ) = lg 3 x = lg 3 lg 7 - lg 3
Løysing på oppgåve 2: Sjå Ida sitt løysingsforslag.
Løysing på oppgåve 3: Sjå Sander sitt løysingsforslag.