Fagartikkel

Faktorisering av andregradsuttrykk ved hjelp av nullpunktmetoden

Vi kan også faktorisere andregradsuttrykk ved ein metode som vi kallar nullpunktmetoden. Vi illustrerer metoden gjennom to eksempel.

Døme 1

Vi ser på andregradsuttrykket $x^{2} - 2 x - 8$ .

Vi startar med å finne nullpunkta.

Vi løyser då likninga $x^{2} - 2 x - 8 = 0$

$\begin{array}{rcl} x^{2} - 2 x - 8 & = & 0 \\ x & = & \frac{- (- 2) \pm \sqrt{{(- 2)}^{2} - 4 \cdot 1 \cdot (- 8)}}{2 \cdot 1} \\ x & = & \frac{2 \pm \sqrt{4 + 32}}{2} \\ x & = & \frac{2 \pm 6}{2} \\ x_{1} & = & \frac{2 - 6}{2} = - 2 \\ x_{2} & = & \frac{2 + 6}{2} = 4 \end{array}$

Uttrykket $x^{2} - 2 x - 8$ er altså lik null når $x = - 2$ og når $x = 4$ .
Ser du at uttrykket $(x - (- 2)) (x - 4) = (x + 2) (x - 4)$ også er lik null når $x = - 2$ og når $x = 4$ ?

Vi multipliserer og ser at

$(x + 2) (x - 4) = x^{2} - 4 x + 2 x - 8 = x^{2} - 2 x - 8$

Vi har då at

$x^{2} - 2 x - 8 = (x + 2) (x - 4)$

Andregradsuttrykket er faktorisert!

Er dette ein metode vi kan bruke for å faktorisere alle andregradsuttrykk?

Vi prøver med eit nytt døme!

Døme 2

Vi ser på uttrykket $2 x^{2} - x - 3$ .

Vi startar igjen med å finne nullpunkta, og løyser likninga $2 x^{2} - x - 3 = 0$ .

$\begin{array}{rcl} 2 x^{2} - x - 3 & = & 0 \\ x & = & \frac{- (- 1) \pm \sqrt{{(- 1)}^{2} - 4 \cdot 2 \cdot (- 3)}}{2 \cdot 2} \\ x & = & \frac{1 \pm \sqrt{25}}{4} \\ x_{1} & = & \frac{1 - 5}{4} = - 1 \\ x_{2} & = & \frac{1 + 5}{4} = \frac{6}{4} = \frac{3}{2} \end{array}$

Uttrykket $2 x^{2} - x - 3$ er altså lik null når $x = - 1$ og når $x = \frac{3}{2}$ .

Vi prøver same metode som i det førre dømet og ser at uttrykket $(x + 1) (x - \frac{3}{2})$ også er lik null når $x = - 1$ og når $x = \frac{3}{2}$ .

Vi multipliserer og får

$(x + 1) (x - \frac{3}{2}) = x^{2} - \frac{3}{2} x + x - \frac{3}{2} = x^{2} - \frac{1}{2} x - \frac{3}{2}$

Dette er ikkje det same andregradsuttrykket som vi starta med.

Vi starta med

$2 x^{2} - x - 3$

Når vi multipliserer ut parentesane, får vi

$x^{2} - \frac{1}{2} x - \frac{3}{2}$

Ser du at vi kan multiplisere det siste uttrykket med $2$ og få det andregradsuttrykket vi starta med?

$(x^{2} - \frac{1}{2} x - \frac{3}{2}) \cdot 2 = 2 \cdot x^{2} - 2 \cdot \frac{1}{2} x - 2 \cdot \frac{3}{2} = 2 x^{2} - x - 3$

Vi har då at

$2 x^{2} - x - 3 = 2 (x + 1) (x - \frac{3}{2})$

Andregradsuttrykket er faktorisert!

Dersom vi ønskjer eit uttrykk utan brøk, kan vi multiplisere 2-talet
inn i den siste parentesen

$2 x^{2} - x - 3 = 2 (x + 1) (x - \frac{3}{2}) = (x + 1) (2 x - 3)$

Vi ser fort at vi må multiplisere med $2$ , fordi det siste uttrykket inneheld leddet $x^{2}$ , mens det polynomet vi starta med, inneheld leddet $2 x^{2}$ .

Den metoden vi har brukt for å faktorisere i dei to døma ovanfor, kallar vi nullpunktmetoden. Du skjønar kanskje kvifor?

Nullpunktmetoden

$a x^{2} + b x + c = a (x - x_{1}) (x - x_{2})$

der $x_{1}$ og $x_{2}$ er løysingane av den generelle andregradslikninga $a x^{2} + b x + c = 0 .$

Utfordring!

Bevis at nullpunktmetoden gjeld generelt ved å vise at $a (x - x_{1}) (x - x_{2}) = a x^{2} + b x + c$

Når det berre finst éi løysing av andregradslikninga, er $x_{1} = x_{2}$ .
Når andregradslikninga ikkje har løysingar, kan ikkje uttrykket faktoriserast.

Vi faktoriserer uttrykket i døme 2 ved CAS i GeoGebra.

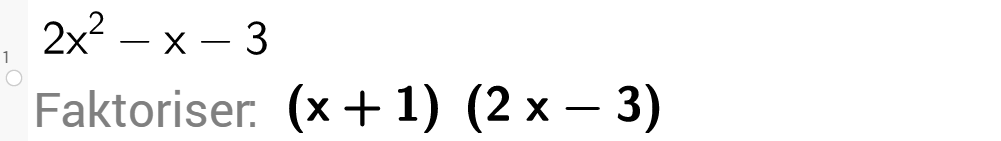
Faktorisering av andregradsuttrykket 2 x i andre minus x minus 3 med kommandoen Faktoriser i GeoGebra. Skjermutklipp. — Bilete: Olav Kristensen / CC BY-NC-SA 4.0

Ikkje gløym at $a$ må vere med i det faktoriserte uttrykket! Kvar har det vorte av talet $a$ framfor parentesane når vi bruker CAS til å faktorisere uttrykket i døme 2?

Video: Tom Jarle Christiansen / CC BY 4.0