Fagstoff

Kvadratsetningane. Konjugatsetninga

Kvadratsetningane er særs sentrale i algebra.

Dei tre kvadratsetningane

Generelt har vi at

$\begin{matrix} (a + b) \cdot (c + d) = a c + a d + b c + b d \end{matrix}$

Korleis blir resultatet dersom parentesuttrykka er like eller nesten like?

Før du les vidare, kan du prøve sjølv å rekne ut uttrykka nedanfor og sjå om du kan finne ein forenkla måte å rekne ut slike uttrykk på.

$(a + b) (a + b) = \begin{matrix} \end{matrix} (a - b) (a - b) = \begin{matrix} \end{matrix} (a + b) (a - b) =$

Den første kvadratsetninga

Når vi multipliserer $(a + b)$ med seg sjølv, får vi kvadratet ${(a + b)}^{2}$ .

$\begin{array}{rcl} {(a + b)}^{2} & = & (a + b) \cdot (a + b) \\ = & a \cdot a + a \cdot b + b \cdot a + b \cdot b \\ = & a^{2} + a b + a b + b^{2} \\ = & a^{2} + 2 a b + b^{2} \end{array}$

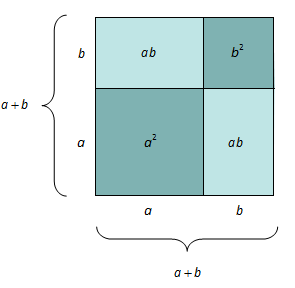
Eit kvadrat med sidekantar a pluss b er delt i fire: eitt kvadrat med sidekantar a, eitt kvadrat med sidekantar b og to rektangel med sidekantar a og b. Illustrasjon. — Bilete: Olav Kristensen, Stein Aanensen / CC BY-SA

Når vi multipliserer ut parentesane, får vi to like ledd, $a b + a b$ , som vi slår saman til $2 a b$ .

Geometrisk ser du at arealet av det store kvadratet ovanfor med sidelengder $a + b$ er lik summen av areala av dei to like store lyse rektangla og dei to mørke kvadrata.

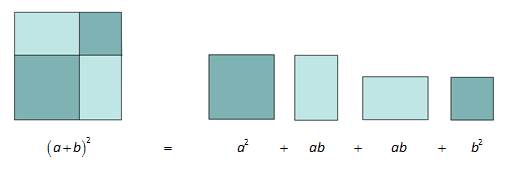
Dette resultatet er kjent som den første kvadratsetninga.

Den andre kvadratsetninga

Eit kvadrat med sidekantar a er delt i fire: eitt kvadrat med sidekantar a minus b, eitt kvadrat med sidekantar b og to rektangel med sidekantar a minus b og b. Illustrasjon. — Bilete: Stein Aanensen, Olav Kristensen / CC BY-NC-SA

Vi multipliserer vidare $(a - b)$ med seg sjølv og får kvadratet ${(a - b)}^{2}$ .

$\begin{array}{rcl} {(a - b)}^{2} & = & (a - b) \cdot (a - b) \\ = & a \cdot a - a \cdot b - b \cdot a + b \cdot b \\ = & a^{2} - a b - a b + b^{2} \\ = & a^{2} - 2 a b + b^{2} \end{array}$

Her får vi to like ledd, $- a b - a b$ , som vi slår saman til $- 2 a b$ .

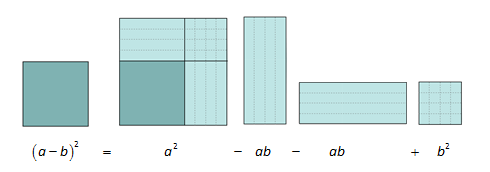
Eit kvadrat med areal parentes a minus b parentes slutt i andre er det same som eitt kvadrat med areal a i andre minus to rektangel med areal a b pluss eitt kvadrat med areal b i andre. Illustrasjon.

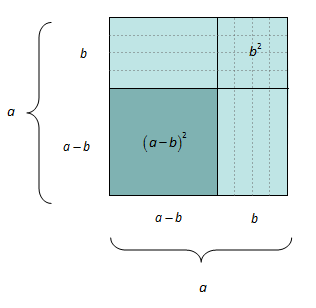
Ser du at vi kan illustrere dette geometrisk dersom vi tek utgangspunkt i eit kvadrat med sider $a$ ?

Dette resultatet er kjent som den andre kvadratsetninga.

Konjugatsetninga

Vi multipliserer så $(a + b)$ med $(a - b)$ .

$\begin{array}{rcl} (a + b) \cdot (a - b) & = & a \cdot a - a \cdot b + b \cdot a - b \cdot b \\ (a + b) \cdot (a - b) & = & a^{2} - a b + a b - b^{2} \\ (a + b) \cdot (a - b) & = & a^{2} - b^{2} \end{array}$

Her får vi ledda $a b$ og $- a b$ , som til saman blir lik null og fell bort.

Ser du at vi kan illustrere dette geometrisk òg ved å starte med eit kvadrat med sidekantar $a$ ?

$a^{2} - b^{2}$ svarer til det lyse området i den første figuren nedanfor.

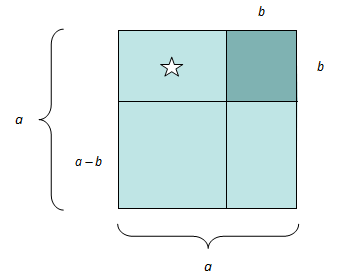
Dersom vi så tenker oss at vi flyttar rektangelet som er merkt med ei stjerne, ser vi at det lyse området òg svarer til $(a + b) (a - b)$ .

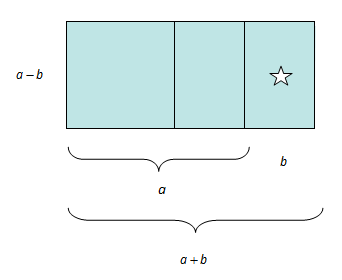
Eit rektangel med sidekantar a minus b og a pluss b. Rektangelet er delt i tre ved at sidekanten som er a pluss b, er delt i tre: b, b og a minus b. Den eine delen med sidekantar b og a minus b er markert med ei stjerne. Illustrasjon.

Dette resultatet er kjent som konjugatsetninga, men blir òg kalla den tredje kvadratsetninga (sjølv om ho ikkje beskriv eit kvadrattal).

Oppsummering

Første kvadratsetning:

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Andre kvadratsetning:

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

Konjugatsetninga:

$(a + b) (a - b) = a^{2} - b^{2}$

Det er freistande å la vere å pugge kvadratsetningane og heller multiplisere kvart ledd i den eine parentesen med kvart ledd i den andre parentesen. Det vil ikkje vere særleg lurt. Kvadratsetningane er nemleg spesielt nyttige til å faktorisere andregradsuttrykk, og då må du bruke dei motsett veg.

Døme på bruk av kvadratsetningane

$\begin{array}{rcl} \begin{array}{rcl} 4 {(x + 2)}^{2} & + & {(2 x - 3)}^{2} - 3 (x - 2) (x + 2) \end{array} \\ = & 4 (x^{2} + 2 \cdot x \cdot 2 + 2^{2}) + ({(2 x)}^{2} - 2 \cdot 2 x \cdot 3 + 3^{2}) - 3 (x^{2} - 2^{2}) \\ = & 4 (x^{2} + 4 x + 4) + (4 x^{2} - 12 x + 9) - 3 (x^{2} - 4) \\ = & (4 x^{2} + 16 x + 16) + (4 x^{2} - 12 x + 9) - (3 x^{2} - 12) \\ = & 4 x^{2} + 16 x + 16 + 4 x^{2} - 12 x + 9 - 3 x^{2} + 12 \\ = & 5 x^{2} + 4 x + 37 \end{array}$

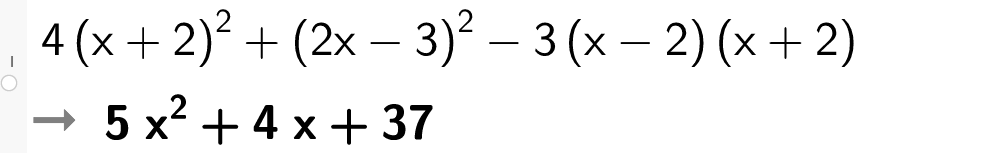
Utklipp frå CAS i GeoGebra. På linje 1 er det skrive 4 parentes x pluss 2 parentes slutt i andre pluss parentes 2 x minus 3 parentes slutt i andre minus 3 parentes x minus 2 parentes slutt parentes x pluss 2 parentes slutt. Resultatet er 5 x i andre pluss 4 x pluss 37. Skjermutklipp.

Med CAS i GeoGebra:

CC BY-SASkrive av Olav Kristensen og Stein Aanensen.

Sist fagleg oppdatert 22.08.2024