Ulikheter med eksponentialuttrykk

Vi ønsker å løse eksponentialulikheten

$2·3^x>3·4^x$

For å finne ut litt om hvordan vi skal gå fram, løser vi først den tilsvarende eksponentiallikningen.

$$ 2·3^x=3·4^x$$

Siden logaritmen til like tall er like, tar vi logaritmen på begge sider.

$$ \begin{array}{rcl} \lg \left(2·3^x\right) & =& \lg \left(3·4^x\right)\\ & & \\ \lg 2+\lg 3^x & =& \lg 3+\lg 4^x\\ & & \\ \lg 2+x·\lg 3 & =& \lg 3+x·\lg 4\\ & & \\ x·\lg 3-x·\lg 4 & =& \lg 3-\lg 2\\ & & \\ x\left(\lg 3-\mathrm{lg4}\right) & =& \lg 3-\lg 2\\ & & \\ x & =& \frac{\lg 3-\lg 2}{\lg 3-\lg 4}\end{array}$$

Hvordan er det så med logaritmene til to tall som er forskjellige?

For å svare på det, må vi se på funksjonen g gitt ved

$g\left(x\right)=\lg x$

Grafen til $g$ vokser for økende verdier av $x$ i hele definisjonsområdet.

Det betyr at hvis $$ a>b$$, så er $$ \lg a>\lg b$$.

På grafen ser du at siden 10 er større enn 2, så er logaritmen til 10 større enn logaritmen til 2.

Motsatt må det da også gjelde at hvis $$ a<b$$, så er $$ \lg a<\lg b$$.

Hvis $\lg a<\lg b$, har vi også

$$ \begin{array}{rcl} \lg a& < & \lg b\\ & & \\ \lg a-\lg b& <& 0\\ & & \\ \lg \frac{a}{b}& <& 0\end{array}$$

I den siste overgangen har vi brukt den andre logaritmesetningen baklengs.

Dette er viktig å vite når vi skal avgjøre om vi må snu ulikhetstegnet eller ikke hvis vi multipliserer eller dividerer med samme tall på begge sider i en ulikhet.

$$ 2·3^x>3·4^x$$

Vi bruker at $$ a>b\Rightarrow \lg a>\lg b$$, og tar logaritmen på begge sider.

$$ \begin{array}{rcl} \lg \left(2·3^x\right)& > & \lg \left(3·4^x\right)\\ & & \\ \lg 2+\lg 3^x& >& \lg 3+\lg 4^x\\ & & \\ \lg 2+x·\lg 3& >& \lg 3+x·\lg 4\\ & & \\ x·\lg 3-x·\lg 4& >& \lg 3-\lg 2\\ & & \\ x\left(\lg 3-\lg 4\right)& >& \lg 3-\lg 2\\ & & \\ x& <& \frac{\lg 3-\mathrm{lg2}}{\mathrm{lg3}-\lg 4}\end{array}$$

Oppgave

Hvorfor snudde vi ulikhetstegnet i den siste overgangen?

Nedenfor kan du se en video der løsningen blir gjennomgått.

I eksempel 2 på siden Eksponentiallikninger fant vi ut hvor lenge et beløp på 1 000 kroner måtte stå i banken for å fordobles når renta var 6 prosent per år. Hvis vi alternativt spør hvor lang tid det tar før beløpet overstiger 2 000 kroner, har vi en ulikhet:

$$ \begin{array}{rcl}1000·1,{06}^x& > & 2·1000\\ & & \\ 1,{06}^x& >& 2\\ & & \\ \lg 10,6^x& >& \lg 2\\ & & \\ x·\lg 1,06& >& \lg 2\\ & & \\ x& >& \frac{\lg 2}{\lg 1,06}\approx 12\end{array}$$

Oppgave

Hvorfor snudde vi ikke ulikhetstegnet i den siste overgangen?

Ved CAS i GeoGebra løser vi først ulikheten eksakt for deretter å finne tilnærmede verdier for løsningen. Det gjør vi ved å trykke direkte på knappen for tilnærmet utregning uten å skrive inn noe i linje 2.

I eksempel 3 i avsnittet om eksponentiallikninger fant vi hvor mange år det ville ta før verdien av Karis bil var sunket til 100 000 kroner. Kari kjøpte bilen for 200 000 kroner. Bilens verdi synker med 10 prosent hvert år.

Hvis vi alternativt spør hvor lang tid det tar før bilens verdi har blitt mindre enn 100 000 kroner, så har vi en ulikhet.

$$ \begin{array}{rcl}200 000·0,{90}^x& < & 100 000\\ & & \\ 0,{90}^x& <& 0,5\\ & & \\ x·\lg 0,90& <& \lg 0,5\\ & & \\ x& \boxed{\stackrel{ }{ }}& \frac{\lg 0,5}{\lg 0,90}\approx 6,6\end{array}$$

Oppgave

Hvilken vei skal ulikhetstegnet stå på den siste linja i løsningen over?

Ved CAS i GeoGebra løser vi først ulikheten eksakt og finner deretter tilnærmet løsning, som vi gjorde i det forrige eksempelet.

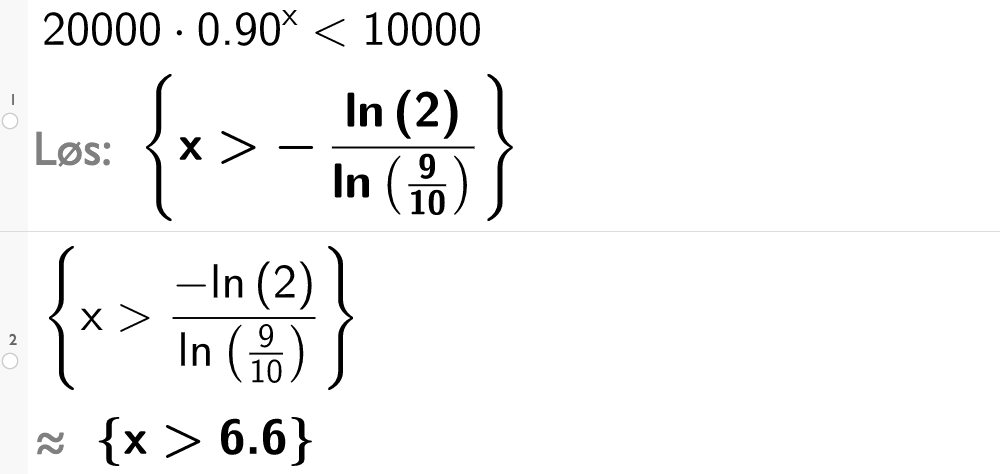
Vi vil løse ulikheten

$\frac{2^{2x}-3·2^x}{x-3}⩾\frac{4}{x-3} x\ne 3$

Vi kan ikke multiplisere $$ x-3$$ med nevneren på begge sider av ulikhetstegnet fordi uttrykket kan være positivt eller negativt alt etter hvilken verdi $x$ har.

Vi må trekke sammen, faktorisere og bruke fortegnsskjema.

$$ \begin{array}{rcl} \frac{2^{2x}-3·2^x}{x-3}& ⩾ & \frac{4}{x-3}\\ & & \\ \frac{2^{2x}-3·2^x}{x-3}-\frac{4}{x-3}& ⩾& 0\\ & & \\ \frac{{\left(2^x\right)}^2-3·2^x-4}{x-3}& ⩾& 0\end{array}$$

Vi setter $$ u=2^x $$ og faktoriserer telleren.

$$ \begin{array}{rcl} u^2-3·u-4 & =& 0\\ & & \\ u & =& \frac{-\left(-3\right)\pm \sqrt{{\left(-3\right)}^2-4·1·\left(-4\right)}}{2·1}\\ & & \\ u & =& \frac{3\pm \sqrt{25}}{2}\\ & & \\ u_1 & =& -1 u_2=4\\ & & \\ \frac{\left(2^x+1\right)\left(2^x-4\right)}{x-3} & ⩾& 0\end{array}$$

Nevneren blir 0 for $$ x=3$$. I telleren kan faktoren $$ 2^x+1 $$ ikke bli 0 eller negativ siden $2^x$ alltid er positiv. Telleren kan derfor bare skifte fortegn når

$\begin{array}{rcl} 2^x-4& = & 0\\ & & \\ 2^x& =& 4\\ & & \\ x·\lg 2& =& \lg 2^2\\ & & \\ x& =& \frac{2\cancel{\lg 2}}{\cancel{\lg 2}}=2\end{array}$

Vi tar "stikkprøver" i intervallene $\langle \leftarrow , 2\rangle , ⟨2, 3⟩ \mathrm{og} ⟨3, \to ⟩$.

For $$ x=0 $$ får vi

$\frac{\left(2^0-4\right)·\left(2^0+1\right)}{0-3}=\frac{\left(1-4\right)·\left(1+1\right)}{-3}=\frac{\left(-3\right)·\left(+2\right)}{-3}$

Uttrykket er positivt.

For $$ x=2,5 $$ får vi

$\frac{\left(2^{2,5}-4\right)·\left(2^{2,5}+1\right)}{2,5-3}=\frac{\left(2^{2,5}-3\right)·\left(2^{2,5}+1\right)}{-0,5}$

Uttrykket er negativt siden $$ 2^{2,5}>2^2=4 \mathrm{siden} 2^x $$alltid vokser.

For $$ x=4 $$ får vi

$\frac{\left(2^4-4\right)·\left(2^4+1\right)}{4-3}=\frac{\left(+12\right)·\left(+17\right)}{+1}$

Uttrykket er positivt.

Nå kan vi tegne fortegnsskjema.

Løsningen på oppgaven blir at $$ x$$ må være mindre enn eller lik 2 eller større enn 3. Løsningen blir

$$ x\in ⟨\leftarrow , 2]\cup \langle 3, \to ⟩$$

Ved CAS i GeoGebra får vi samme løsning. Legg merke til at GeoGebra her ikke forenkler brøken i svaret til 2 når vi prøver å løse ulikheten eksakt, se linje 1. Dette blir kanskje løst i en senere versjon av programmet.