Njuike sisdollui
Bargobihttá

Vinkler

I disse oppgavene skal du finne riktige begreper og komme fram til noen sammenhenger.

2.1.5

a) Hva kalles to linjer som ligger i samme plan og ikke skjærer hverandre?

b) Hva kalles en vinkel på 90°?

c) Hva kalles en vinkel mellom 0° og 90°?

d) Hva kalles en vinkel mellom 90° og 180°?

e) Hva kalles to vinkler som til sammen er 90°?

f) Hva kalles to vinkler som til sammen er 180°?

Løsning

a) parallelle

b) rett

c) spiss

d) stump

e) komplement

f) supplement

2.1.6

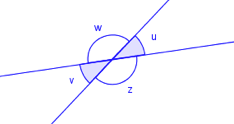
Hva er sammenhengene mellom vinklene nedenfor? Bruk figuren og finn begrepene.

Ei linje gjennom punktene A og B og ei annen linje gjennom punktene C og D krysser hverandre i punktet E. Vinkel B E D er 50 grader. Illustrasjon.
Govva: Stein Aanensen, Olav Kristensen / CC BY-SA 4.0

a) Hvilken type vinkler er ∠AEC og ∠DEB ?

b) Hvilken type vinkler er ∠AED og ∠CEB ?

c) Hvilken type vinkler er ∠AEC og ∠CEB ?

d) Hvilken type vinkler er ∠AED og ∠DEB?

Løsning

a) toppvinkler

b) toppvinkler

c) supplementvinkler

d) supplementvinkler

2.1.7

To parallelle linjer b og c krysses av ei tredje linje. Den spisse vinkelen mellom linja b og linja som krysser, er 50 grader. Den andre vinkelen har navnet w. De spisse vinklene mellom linja c og linja som krysser, kalles u og v. Én av de andre vinklene kalles alfa. Illustrasjon.
Govva: Stein Aanensen, Olav Kristensen / CC BY-SA 4.0

Linjene b og c på figuren er parallelle. Bestem vinkel u, v, w og a.

Løsning

u=50°,v=50°, w=180° -50°=130°, a=130°

2.1.8

To linjer krysser hverandre. De spisse vinklene mellom linjene kalles u og v. De to andre vinklene kalles w og z. Illustrasjon.
Govva: Stein Aanensen, Olav Kristensen / CC BY-SA 4.0

Vis at  w=z.

Løsning

v+w = 180°      w=180°-vz+v=180°      z=180°-vw=z

2.1.9

Forklar hvorfor  u=v.

To stråler møtes og danner vinkelen u. Den ene strålen står vinkelrett på ei linje, den andre strålen står vinkelrett på ei annen linje. De to linjene møtes og danner vinkelen v. Illustrasjon.
Govva: Bjarne Skurdal / CC BY-SA 4.0
Løsning

Her blir det lettest å forklare hvis vi setter navn på noen punkter:

To stråler møtes i punktet A og danner vinkelen u. Den ene strålen står vinkelrett på ei linje i punktet B, den andre strålen står vinkelrett på ei annen linje i punktet E. De to linjene møtes i punktet D og danner vinkelen v. Linjestykket B D skjærer linjestykket A E i punktet C. Linja gjennom A og B skjærer linja gjennom D og E i punktet F. Illustrasjon.
Govva: Tove Annette Holter / CC BY-SA 4.0

Denne oppgaven kan løses på flere måter:

1.
Vi ser på trekantene ABC og CDE. Begge disse trekantene har en rett vinkel. I tillegg ser vi at vinklene ACB og ECD er toppvinkler og dermed like.

Vinkelsummen i en trekant er 180°. Vi har derfor at  u=v.

2.
Vi ser på trekantene AEF og BDF. Begge disse trekantene har en rett vinkel. I tillegg deler de vinkel F. På samme måte som i løsning nummer 1 får vi at  u=v.

3.
Vinkelbeinet AB til u står vinkelrett på vinkelbeinet CD til v. Det andre vinkelbeinet til u, AC, står vinkelrett på det andre vinkelbeinet til v, DE. Etter setningen om vinkelbein som parvis står vinkelrett på hverandre, må  u=v.