Bargobihttá

Å bruke valgtre for å beregne sannsynlighet

Her kan du løse oppgaver der du får bruk for valgtre.

4.1.70

Vi kaster en tikrone tre ganger.

a) Tegn et valgtre som illustrerer de mulige utfallene vi kan få.

Vis fasit

Valgtre. Øverst står det Myntkast. Det går to greiner ned herfra, og disse er merket M for mynt og K for krone. Fra M går det så ned to greiner, og disse er merket MM og MK. Fra K går det ned to greiner som er merket KM og KK. Fra hver av disse greinene går det ned to greiner, så på nederste nivå ender det med til sammen åtte alternativer: MMM, MMK, MKM, MKK, KMM, KMK, KKM og KKK. Illustrasjon. — Govva: Olav Kristensen, Stein Aanensen / CC BY-SA 4.0

b) Hva er sannsynligheten for å få nøyaktig to mynter?

Vis fasit

Vi har åtte ulike utfall. I tre av utfallene får vi nøyaktig to mynter.

Sannsynligheten for nøyaktig to mynter blir $P (2 mynt) = \frac{3}{8}$ .

Her kan vi bruke "gunstige delt på mulige"-regelen siden alle utfall er like sannsynlige (uniform sannsynlighetsmodell).

c) Hva er sannsynligheten for å ikke få krone noen av gangene?

Vis fasit

Sannsynligheten for ingen krone er det samme som sannsynligheten for bare mynter: $P (M M M) = \frac{1}{8}$ .

4.1.71

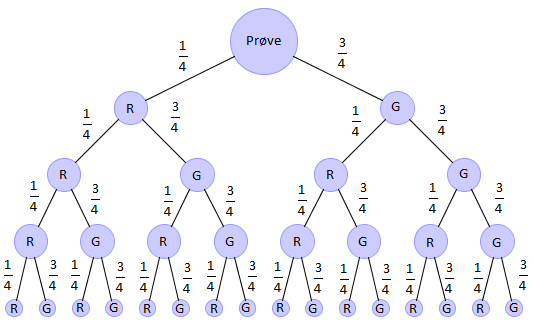
Tenk deg en prøve i matematikk med fire oppgaver. På hver av oppgavene skal du krysse av i én av fire ruter for rett svar. Du er ikke forberedt, og alle svaralternativene virker like sannsynlige, så du bare gjetter.

a) Tegn et valgtre som illustrerer de mulige utfallene vi kan få.

Vis fasit

Valgtre som viser mulige utfall på en prøve. Illustrasjon. — Govva: Stein Aanensen, Olav Kristensen / CC BY-NC-SA 4.0

b) Hva er sannsynligheten for å få fire rette svar?

Vis fasit

$P (R R R R) = \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} = \frac{1}{256}$

c) Hva er sannsynligheten for å få tre rette svar?

Vis fasit

Her gjelder det å finne alle rutene fra toppen av valgtreet og helt ned som er innom tre rette svar (og ett galt svar).

$\begin{array}{rcl} P (3 rette) & = & P (R R R G) + P (R R G R) + P (R G R R) + P (G R R R) \\ = & 4 \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{3}{4} = \frac{3}{64} \end{array}$

d) Hva er sannsynligheten for å få to rette svar?

Vis fasit

Her må vi finne alle rutene fra toppen av valgtreet og helt ned som er innom to rette svar (og to gale svar). Det er seks slike ruter.

$P (2 rette) = 6 \cdot \frac{1}{4} \cdot \frac{1}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} = \frac{27}{128}$

e) Hva er sannsynligheten for å få ett rett svar?

Vis fasit

Her må vi finne alle rutene fra toppen av valgtreet og helt ned som er innom ett rett svar (og tre gale svar). Det er fire slike ruter.

$P (1 rett) = 4 \cdot \frac{1}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} = \frac{27}{64}$

f) Hva er sannsynligheten for å få ingen rette svar?

Vis fasit

$P (G G G G) = \frac{3}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} \cdot \frac{3}{4} = \frac{81}{256}$

4.1.70

4.1.71

Njuolggadusat teavstta geavaheapmái "Å bruke valgtre for å beregne sannsynlighet"