Multiplikasjon av sannsynligheter - Matematikk S1 - NDLA

Fágaartihkal

Multiplikasjon av sannsynligheter

For å finne sannsynligheten til sammensatte hendelser kan vi multiplisere sannsynligheten for enkelthendelsene. Vi må ta hensyn til om hendelsene er avhengige eller uavhengige.

Produktsetningen for uavhengige hendelser

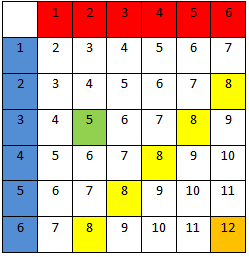
Tabell som viser summen av ett kast med to terninger for alle mulige utfall. Illustrasjon.

Vi har tidligere sett på forsøket "kast med to terninger".

Ved å bruke regelen om gunstige over mulige kan vi finne sannsynligheten for å få summen 12, det vil si sekser på begge terningene.

$å$

Sannsynligheten for å få en sekser når vi kaster den røde terningen, er . Sannsynligheten for å få en sekser når vi kaster den blå terningen, er også . Dette gjelder uavhengig av om det ble en sekser på rød terning eller ikke. Om vi kaster rød terning først og får en sekser, endrer ikke dette sjansene for å få en sekser på den blå terningen.

Vi sier at hendelsene "å få sekser på rød terning" og "å få sekser på blå terning" er uavhengige hendelser.

Vi så ovenfor at sannsynligheten for å få sekser i begge kastene er lik . Denne sannsynligheten får vi også ved å multiplisere sannsynlighetene for å få sekser på hver av terningene.

$å ø å å å ø å å$

Dette gjelder generelt og kalles produktsetningen for uavhengige hendelser.

To hendelser er uavhengige hvis en opplysning om at den ene har inntruffet ikke endrer sannsynligheten for at den andre skal inntreffe.

For to uavhengige hendelser og er

og betyr her at både og inntreffer.

Vi erstatter ordet "og" med symbolet "", og leses som

" snitt ". Vi får

Setningen gjelder også for en serie av hendelser.

Tippekupong

Utsnitt fra tippekupong som viser en tabell over 12 ulike fotballkamper, for det meste med engelske lag. Til høyre kan man krysse av for H, U eller B på alle kampene. Foto.

Hvor stor er sannsynligheten for å få 12 rette i fotballtipping når vi fyller ut éi rekke på en tippekupong helt tilfeldig?

Løsning

Vi kan oppfatte dette som 12 hendelser. Hver kamp kan ende med hjemmeseier (H), uavgjort (U) eller borteseier (B). I hver kamp er sannsynligheten for å tippe rett lik .

Sannsynligheten for å tippe rett i hver kamp er den samme uavhengig av om vi har tippet rett eller feil i tidligere kamper.

Vi har altså 12 uavhengige hendelser.

Sannsynligheten for å tippe 12 rette er da lik multiplisert med seg selv 12 ganger.

Under kan du se en film som viser produktsetningen for uavhengige hendelser.

Video: Olav Kristensen / CC BY-NC-SA 4.0

Betinget sannsynlighet – den generelle produktsetningen

Caps med lapper med tall snudd opp ned. Foto.

Celine og Maren trekker hver sin lapp fra en hatt som inneholder fem lapper med tallene fra 1 til 5.

Vi definerer hendelsen.

: På Celines lapp står det et partall.
: På Marens lapp står det et partall.

Hvis Celine trekker den første lappen, er det i hatten 2 lapper med partall og 3 lapper med oddetall. Sannsynligheten for å trekke en lapp med partall er

Hvis Celine trekker et partall, er det igjen 1 lapp med partall og 3 lapper med oddetall når Maren trekker, og sannsynligheten for at Maren også trekker et partall, er lik .

Hvis Celine ikke trekker et partall, er det igjen 2 lapper med partall og 2 lapper med oddetall når Maren trekker, og sannsynligheten for at Maren trekker et partall, er lik .

Sannsynligheten for avhenger av om hendelsen inntreffer eller ikke. Vi sier at hendelsene og er avhengige.

Sannsynligheten for at inntreffer når vi vet at har inntruffet, er lik .

Sannsynligheten for at inntreffer når vi vet at ikke har inntruffet, er lik .

Vi kaller dette betinget sannsynlighet. Vi bruker skrivemåten , som vi leser som "sannsynligheten for gitt ". Vi har at

Vi bruker skrivemåten for ikke . Da er

Sannsynligheten for at det skal stå et partall på begge lappene, det vil si at både hendelse og hendelse inntreffer, finner vi ved å multiplisere sannsynlighetene:

Hvis Maren trekker den første lappen, gjelder tilsvarende at

Tilsvarende blir nå

Sannsynligheten for at det skal stå et partall på begge lappene, det vil si at både hendelse og hendelse inntreffer, finner vi ved å multiplisere sannsynlighetene:

Betinget sannsynlighet

Sannsynligheten for at inntreffer når vi vet at har inntruffet, skriver vi som , og det leses som "sannsynligheten for gitt ". Vi kaller det for betinget sannsynlighet.

Den generelle produktsetningen for sannsynligheter

Sannsynligheten for at to hendelser, både og skal inntreffe, er

For uavhengige hendelser er .

Under kan du se en film om betinget sannsynlighet.

Video: Olav Kristensen / CC BY-NC-SA 4.0