Binomisk sannsynlighetsmodell

Du skal ha matteprøve. Du er ikke forberedt, og alle svaralternativene virker like sannsynlige. Vi går ut fra at de ulike oppgavene er uavhengige av hverandre. Det vil si at hva du svarer på én oppgave, ikke påvirker svaret på den neste.
Du krysser av helt tilfeldig. Sannsynligheten for å svare riktig på en oppgave er da , og sannsynligheten for å svare galt er .
Hva er sannsynligheten for å få null, ett, to, tre og fire riktige svar?
Det er bare én måte du kan få fire riktige svar på. Vi lar stå for at svaret er riktig, og stå for at svaret er galt.
Det er også bare én måte du kan få null riktige svar på.
Men på hvor mange måter kan du få to riktige svar?
Sannsynligheten for å svare riktig på de to første oppgavene (og galt på de to neste) er
Men det er flere måter å få to riktige svar på. Du kan for eksempel svare riktig på de to siste oppgavene (), på første og siste oppgave () og så videre.
For å telle opp hvor mange måter det er, kan du lage et valgtre. Vi starter øverst på midten. For den første oppgaven tegner vi to streker på skrå nedover i hver sin retning. Den ene streken er for riktig svar, den andre for feil svar – altså én strek for hvert valg. Vi skriver også på sannsynligheten for hvert enkelt valg ved sida av valget.
Fra enden på hvert av disse to valgene tegner vi to nye streker for den andre oppgaven, for riktig og for feil svar. Nå vil antallet streker doble seg for hver ny oppgave, og vi får en trestruktur. Etter fire oppgaver vil vi ha greiner på valgtreet.
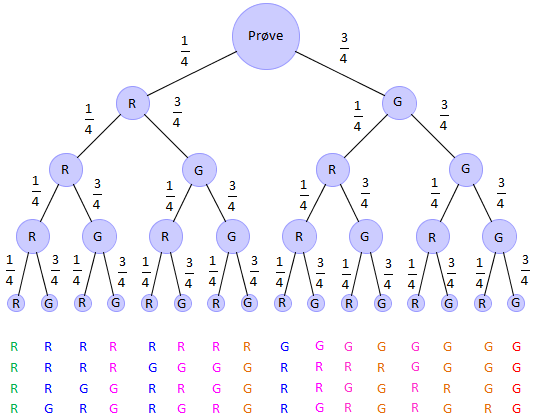
Valgtreet over viser hvor mange måter du kan få null, ett, to, tre og fire riktige svar på. Vi teller opp og samler resultatene i en tabell.
Antall rette (X = | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
Antall måter | 1 | 4 | 6 | 4 | 1 |
Antall måter |
Legg merke til at dette er fjerde rad i Pascals trekant.
At binomialkoeffisientene dukker opp her, er ikke så underlig. Å finne antallet måter å få to rette svar på er det samme som å finne ut på hvor mange måter vi kan velge to plasser av fire hvor det skal stå .
Vi legger merke til at alle stiene gjennom valgtreet som gir to riktige svar, har lik sannsynlighet, nemlig
På sida Tre ulike typer utvalg kan du se at vi kan bruke binomialkoeffisienter for å regne ut antallet kombinasjoner ved denne typen utvalg. Vi får altså at
På samme måte vil da
Sammensatte forsøk som dette kaller vi binomiske forsøk. Antall rette svar er en stokastisk variabel. I vårt eksempel kan denne variabelen ha verdien 0, 1, 2, 3 eller 4. Vi kan da skrive et generelt uttrykk for sannsynlighetsfordelingen slik:
Her er
Dette gjelder helt generelt. Vi antar at vi har en prøve med
Alle oppgavene har like mange svaralternativ, derfor er sannsynligheten for å svare riktig lik hele tida. Vi kan kalle denne sannsynligheten for
Antall riktige svar er den stokastiske variabelen
Andre eksempler på binomiske forsøk

Å kaste en terning et bestemt antall ganger og se om vi får sekser eller ikke på hvert enkelt kast, er et annet eksempel på et binomisk forsøk. Vi kan bruke formelen ovenfor til å beregne sannsynligheten for å få et bestemt antall seksere.

Å kaste en mynt et bestemt antall ganger og se om vi får «krone» eller «mynt» på hvert enkelt kast, er også et eksempel på et binomisk forsøk. Vi kan bruke formelen ovenfor til å beregne sannsynligheten for å få et bestemt antall «krone».
Begge disse eksemplene skal du få prøve deg på i oppgavene senere.
Vi kan bruke sannsynlighetskalkulatoren i GeoGebra til å regne ut binomisk sannsynlighet.
En flervalgsprøve har fem oppgaver med fire svaralternativer på hver oppgave. Du besvarer flervalgsprøven ved ren gjetning.
Først ser vi på hvordan du kan finne sannsynligheten for å svare riktig på akkurat én av oppgavene. Du velger «Binomisk fordeling» og fyller inn som vist nedenfor.
Så ser vi hvordan du kan finne sannsynligheten for å få mer enn to riktige svar:
Vi kan importere binom fra scipy.stats. Her har vi en metode binom.pmf() som gir oss den binomiske fordelingen. Metoden har tre argumenter. Det første argumentet er en liste over de verdiene av den stokastiske variabelen vi ønsker å finne sannsynligheten for. De to neste er
1from scipy.stats import binom 2 3n = 5 4p = 0.25 5X = [] #lager en liste med verdiene til den stokastiske variabelen 6 7for i in range(n+1): 8 X.append(i) #legger inn alle de mulige verdiene til X 9 10rettesvar = binom.pmf(X,n,p) #lager en array med sannsynlighetsfordelingen 11 12for i in rettesvar: 13 print(i) #skriver sannsynlighetsfordelingen i en kolonne
Hvis vi ikke ønsker hele fordelingen, men for eksempel ønsker å finne sannsynligheten for å få to eller tre rette svar, setter vi inn lista [2,3] som første argument i binom.pmf(). Vi kan også bruke metoden sum() for å finne den samlede sannsynligheten.
1 2from scipy.stats import binom 3 4n = 5 5p = 0.25 6 7rettesvar = binom.pmf([2,3],n,p) 8 9for i in rettesvar: 10 print(i) 11 12print(sum(rettesvar)) #vi finner summen av sannsynlighetene for 2 og 3
Kopier programmene til din editor, og kjør dem!
Oppsummering
For at et forsøk med
- Alle delforsøkene må være uavhengige av hverandre.
- Vi må ha bare to utfall (bi betyr to!), der det ene betegnes som suksess.
- Vi må ha lik sannsynlighet (
p
Dersom alle disse kriteriene er oppfylt, kan vi finne sannsynligheten for de ulike verdiene